


Números triangulares quadrados perfeitos são números que ao mesmo tempo são números triangulares e quadrados.
Números quadrados cúbicos perfeitos são números que ao mesmo tempo são números quadrados e cúbicos.
O presente estudo demonstra métodos de se gerarem ternos pitagóricos em que os termos aparecem números: triangulares, triangulares quadrados, cúbicos e quadrados cúbicos.
O Número 6 é um número prá lá de especial, além de ser o Primeiro Número Perfeito possui diversas outras propriedades matemáticas, vejamos:
a) é o primeiro número que é produto de 2 números primos consecutivos;
2 x 3 = 6
Números que são produtos de 2 números primos consecutivos possuem divisores em quantidades de números quadrados perfeitos com os quais são possíveis de se construirem quadrados mágicos multimágicos múltiplicativos sequenciais.
b) o seu quadrado 36 é número triangular quadrado perfeito;
c) o seu quadrado 36 é raiz cúbica do número 46656 que é número quadrado cúbico;
d) o seu cubo 216 é raiz quadrada do número 46656 que é número quadrado cúbico;
E como veremos a seguir, o 6 faz parte do primeiro Terno Pitagórico em que nos termos aparecem números triangulares e número cúbico e cujos quadrados são quadrados de triangulares e quadrado de um cubo.
Euclides, em seu livro Elementos, demonstrou que existe uma infinidade de ternos pitagóricos primitivos. Além disso, encontrou fórmulas que geram todos os ternos pitagóricos primitivos. Dados dois números naturais m>n, o terno (a,b,c), onde:
a = m² - n²
b = 2mn
c = m² + n²
é pitagórico, e é primitivo se e somente se m e n são primos entre si e possuem paridades distintas.
Fonte: https://pt.wikipedia.org/
onde:
m > n (m tem que ser maior que n)
m e n tem que ser primos entre si
Observação importante:
a) as Fómulas de Euclides geram ternos pitagóricos derivados que são o dobro, do dobro, do dobro ... e assim sucessivamente de ternos pitagóricos primitivos;
b) as Fórmulas de Euclides não geram ternos pitagóricos derivados ímpares.
Tanto aqui no WebSite Os Fantásticos Números Primos quanto no livro digital Ternos Pitagóricos e Sequências Numéricas também há diversos estudos sobre as Fórmulas de Euclides, bem como, outros métodos para se gerarem ternos pitagóricos.
Escolhendo-se 2 números triangulares consecutivos e os substituindo nas Fórmulas de Euclides, obtêm-se ternos pitagóricos em que entre os termos apresentam números: triangulares, cúbicos, triangulares quadrados, bem como, quadrados cúbicos, vejamos:
| Fórmulas de Euclides | |||||||||
| m | n | m^2 | n^2 | m^2 - n^2 | 2mn | m^2 + n^2 | a^2 | b^2 | c^2 |
| a | b | c | |||||||
| 3 | 1 | 9 | 1 | 8 | 6 | 10 | 64 | 36 | 100 |
| www.osfantasticosnumerosprimos.com.br | |||||||||
Fonte: Tabela adaptada de: SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas
a) 8 é cúbico;
b) 6 e 10 são triangulares;
c) 36 é triangular quadrado;
d) 64 é quadrado cúbico;
e) 100 é quadrado de triangular;
f) Terno Pitagórico Derivados 6 - 8 - 10.
| Fórmulas de Euclides | |||||||||
| m | n | m^2 | n^2 | m^2 - n^2 | 2mn | m^2 + n^2 | a^2 | b^2 | c^2 |
| a | b | c | |||||||
| 6 | 3 | 36 | 9 | 27 | 36 | 45 | 729 | 1296 | 2025 |
| www.osfantasticosnumerosprimos.com.br | |||||||||
Fonte: Tabela adaptada de: SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas
a) 27 é cúbico;
b) 36 e 45 são triangulares;
c) 36 é triangular quadrado;
d) 729 é quadrado cúbico;
e) 2025 é quadrado de triangular.
f) Terno Pitagórico Derivados 27 - 36 - 45.
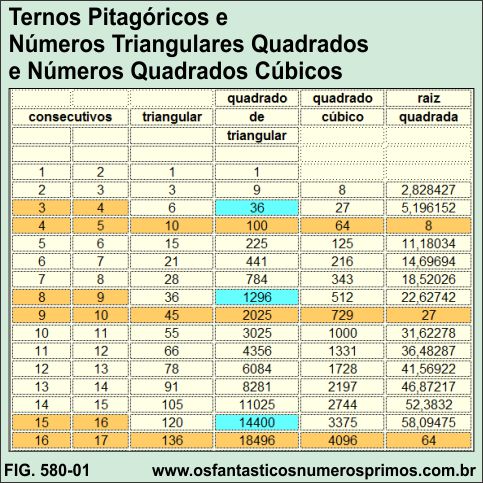
A tabela a seguir têm as seguintes características construtivas:
a) o produto de 2 números consecutivos (colunas A) dividido por 2 tem como resultado um número triangular (coluna B);
b) Coluna C são números quadrados perfeitos da Coluna B;
c) Coluna D são as diferenças de números quadrados de triangulares da coluna C;
d) Coluna E são raízes quadradas da Coluna D,...
... as quais apresentam as seguintes propriedades relacionadas a ternos pitagóricos cujos termos há números triangulares, triangulares quadrados e quadrados cúbicos:
| Números Triangulares, | |||||
| Triangulares Quadrados e | |||||
| Quadrados Cúbicos | |||||
| números | |||||
| A | B | C | D | E | |
| quadrado | quadrado | raiz | |||
| consecutivos | triangular | de | cúbico | quadrada | |
| triangular | de | ||||
| (diferença) | D | ||||
| 1 | 2 | 1 | 1 | ||
| 2 | 3 | 3 | 9 | 8 | 2,828427 |
| 3 | 4 | 6 | 36 | 27 | 5,196152 |
| 4 | 5 | 10 | 100 | 64 | 8 |
| 5 | 6 | 15 | 225 | 125 | 11,18034 |
| 6 | 7 | 21 | 441 | 216 | 14,69694 |
| 7 | 8 | 28 | 784 | 343 | 18,52026 |
| 8 | 9 | 36 | 1296 | 512 | 22,62742 |
| 9 | 10 | 45 | 2025 | 729 | 27 |
| 10 | 11 | 55 | 3025 | 1000 | 31,62278 |
| 11 | 12 | 66 | 4356 | 1331 | 36,48287 |
| 12 | 13 | 78 | 6084 | 1728 | 41,56922 |
| 13 | 14 | 91 | 8281 | 2197 | 46,87217 |
| 14 | 15 | 105 | 11025 | 2744 | 52,3832 |
| 15 | 16 | 120 | 14400 | 3375 | 58,09475 |
| 16 | 17 | 136 | 18496 | 4096 | 64 |
| 17 | 18 | 153 | 23409 | 4913 | 70,0928 |
| 18 | 19 | 171 | 29241 | 5832 | 76,36753 |
| 19 | 20 | 190 | 36100 | 6859 | 82,81908 |
| 20 | 21 | 210 | 44100 | 8000 | 89,44272 |
| 21 | 22 | 231 | 53361 | 9261 | 96,23409 |
| 22 | 23 | 253 | 64009 | 10648 | 103,1891 |
| 23 | 24 | 276 | 76176 | 12167 | 110,3041 |
| 24 | 25 | 300 | 90000 | 13824 | 117,5755 |
| 25 | 26 | 325 | 105625 | 15625 | 125 |
| 26 | 27 | 351 | 123201 | 17576 | 132,5745 |
| 27 | 28 | 378 | 142884 | 19683 | 140,2961 |
| 28 | 29 | 406 | 164836 | 21952 | 148,1621 |
| 29 | 30 | 435 | 189225 | 24389 | 156,1698 |
| 30 | 31 | 465 | 216225 | 27000 | 164,3168 |
| 31 | 32 | 496 | 246016 | 29791 | 172,6007 |
| 32 | 33 | 528 | 278784 | 32768 | 181,0193 |
| 33 | 34 | 561 | 314721 | 35937 | 189,5706 |
| 34 | 35 | 595 | 354025 | 39304 | 198,2524 |
| 35 | 36 | 630 | 396900 | 42875 | 207,0628 |
| 36 | 37 | 666 | 443556 | 46656 | 216 |
| www.osfantasticosnumerosprimos.com.br | |||||
| A | B | C | D | E | |
| quadrado | quadrado | raiz | |||
| consecutivos | triangular | de | cúbico | quadrada | |
| triangular | |||||
| 3 | 4 | 6 | 36 | 27 | 5,196152 |
| 4 | 5 | 10 | 100 | 64 | 8 |
a) nas duplas de números consecutivos há o quadrado perfeito 4;
b) 3 é a ordem / posição do triangular 6;
c) 4 é a ordem / posição do triangular 10;
d) 6 e 10 são triangulares;
e) 36 é um triangular quadrado perfeito;
f) 8 e 64 são números cúbicos;
g) 64 é um quadrado perfeito cúbico;
6^2 = 36
8^2 = 64
10^2 = 100
A soma de 36 (triangular quadrado) mais 64 (quadrado cúbico) é igual ao quadrado 100.
| A | B | C | D | E | |
| quadrado | quadrado | raiz | |||
| consecutivos | triangular | de | cúbico | quadrada | |
| triangular | |||||
| 8 | 9 | 36 | 1296 | 512 | 22,62742 |
| 9 | 10 | 45 | 2025 | 729 | 27 |
a) nas duplas de números consecutivos há o quadrado perfeito 9;
b) 8 é a ordem / posição do triangular 36;
c) 9 é a ordem / posição do triangular 45;
d) 36 e 45 são triangulares;
e) 36 é um triangular quadrado perfeito;
f) 729 e 27 são números cúbicos;
g) 729 é um quadrado perfeito cúbico;
27^2 = 729
36^2 = 1296
45^2 = 2025
A soma de 729 (triangular quadrado) mais 1296 (quadrado de triangular) é igual ao quadrado 2025.
Esta demonstração de formação do Terno Pitagórico 216 - 630 - 666 foi enviada pelo Professor de Química Fernando Manso, da Universidade Tecnológica Federal do Paraná - UTFPR-CM, cujo teor do E-mail é:
" É sempre possível escrever cubos como diferença de quadrados.
Se esse cubo é um quadrado perfeito, temos então um terno Pitagórico.
O mais interessante é que todo cubo pode ser escrito como a diferença de dois quadrados de números triangulares consecutivos.
n^3 =[T(n)]^2 - [T(n-1)]^2.
Para termos um Terno Pitagórico basta que n seja um quadrado perfeito.
Assim, (n^2)^3 = [T(n^2 )]^2 - [T(n^2 - 1)]^2;
Como (n^2)^3 = (n^3)^2, temos o seguinte terno Pitagórico:
[T(n^2 )]^2 = (n^3)^2 + [T(n^2 - 1]^2.
Ex: n = 6;
T(36) = 666;
T(35) = 630;
6^3 = 216;
Portanto 666^2 = 630^2 + 216^2;
443556 = 396900 + 46656 = 443556."
O Professor apresenta também algumas curiosidades matemáticas:
"Não bastasse T(36) = 666, 666^2 = 443556 é um número bem curioso:
1) a soma de seus dígitos é um cubo perfeito (4+4+3+5+5+6) = 27 = 3^3;
2) dividindo 443556 em dois números de 3 dígitos,
a soma desses números na ordem direta e inversa dão o mesmo resultado igual a 999: ( 443 + 556 = 655 + 344 = 999 );
3) A sequência 355 / ( 556 - 443 ) = ( Pi );
4) A soma dos dígitos pode ser dada pela soma de três números consecutivos do centro para a extremidade: 8 + 9 + 10 = ( 3 + 5 ) + ( 4 + 5 ) + ( 4 + 6 ) e, o produto desses 3 números é igual a 6!;
8 x 9 x 10 = 720 = 1 x 2 x 3 x 4 x 5 x 6 = 6!;
5) ( 4! + 4! + 3! + 5! + 5! + 6! ) = 1014;
(1 + 0 ) = 1;
(4 + 1 + 0 ) = 5;
( 1 + 0 + 1 + 4 ) = 6;
1014 = 13^2 x 6;
156 = 13 x 2 x 6;
6) 666 x 999 = 665334 que tem as mesmas propriedades que 443556, exceto que a razão 533 / 665 - 334 é uma aproximação para o número de ouro e não para Pi.
Ternos pitagóricos em que entre os termos há números triangulares, triangulares quadrados, cúbicos, quadrados cúbicos podem ser formados a partir:
a) de 2 números triangulares consecutivos com as Fórmulas de Euclides;
b) de 2 grupos de números consecutivos (em que dois termos são quadrados perfeitos) com expressões numéricas;
c) de 2 números consecutivos, sendo um quadrado perfeito e o seu antecessor e utilizando o Método do Professor Fernando Manso.
Autor: Ricardo Silva - agosto/2025
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato