logotipo os fantasticos numeros primos
capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo
Página de estudos de matemática e sequências numéricas

Ternos Pitagóricos e o Método de Potências - 578

"A primeira descoberta de natureza aritmética foram os ternos pitagóricos; descoberta essa encontrada em um fragmento de uma tabela: a tábua de argila quebrada Pimpliton 322 (Larsa, Mesopotâmia, cerca de 1800 a.C.) que contém uma lista de "ternos pitagóricos", ou seja, inteiros (a, b, c) tais que a2 + b2 = c2. Os ternos são muitos e bastante elevados para terem sido obtidos pela força bruta.

Se algum outro método foi utilizado os ternos foram inicialmente construídos e depois reordenados por (a, b, c), presumidamente para uso como uma 'tabela", ou seja, com vista às suas aplicações.

Os escritores da história da matemática não sabem o que essas aplicações podem ter sido, ou se poderia ter havida qualquer uma; a astronomia babilônica, por exemplo, realmente floresceu só mais tarde. Tem sido sugerido, em vez disso, que a tabela fosse uma fonte de exemplos numéricos para problemas escolares."

O grifo é nosso.

Fonte: NASCIMENTO, Sebastião Vieira do. Desvendando os segredos do triângulo retângulo e descobrindo curisosidades até hoje não conhecidas.

Ternos Pitagóricos e o Método de Potências

Diversos são os métodos numéricos e fórmulas para se gerarem ternos pitagóricos.

Tanto aqui no WebSite Os Fantásticos Números Primos quanto no livro digital Ternos Pitagóricos e Sequências Numéricas também há diferentes exemplos de métodos.

No referido livro acima, do Professor Sebastião Vieira do Nascimento, carinhosamente conhecido por Professor Sebá, os estudos de ternos pitagóricos envolvem sequências numéricas, bem como, ternos pitagóricos com figuras geométricas.

O presente estudo demonstra o novíssimo Método de Potências para se gerarem ternos pitagóricos, desenvolvidas pelo Professor de Química Fernando Manso, da Universidade Tecnológica Federal do Paraná - UTFPR-CM, vejamos:

E-mail - data: 27/07/205

"Olá Ricardo, bom dia!

Veja que interessante.

O produto n x n^3 = n^4 = (n^2)^2, portanto um quadrado perfeito.

Ex: 3^3 x 3 = 3^4 = (3^2)^2 = 9^2 = 81.

É sempre possível escrever um quadrado perfeito como a diferença de dois quadrados perfeitos.

O interessante é que isso constitui um terno Pitagórico.

Como construir esses ternos Pitagóricos:

seja a e b números naturais com a > b. a^2 - b^2 = (a+b).(a-b) = n^3 . n .

Precisamos então achar dois números a e b cuja soma seja n^3 e cuja diferença seja n.

1) se n^3 for par, divida por 2; se n^3 for ímpar, divida por 2 e arredonde o valor para cima para o a e arredonde o valor para baixo para o b.

2) se n^3 for par, a e b terão o mesmo valor depois do passo 1; se n^3 for ímpar você terá a=b+1. a partir daí aumente 1 unidade para a e diminua 1 unidade para b até que a-b seja igual a n.

3) encontrados a e b no passo 2, faça a^2 - b^2 = (n^3) . n; some b^2 dos lados da equação e você terá um terno Pitagórico: a^2 = b^2 + (n^3).n = b^2 + (n^2)^2.

Vamos fazer o exemplo do (3^3).3, passo a passo.

1) 3^3 = 27/2, a=14; b=13. a diferença entre eles é igual a 1, precisamos que essa diferença seja igual a 3; passo

2) a=14+1 = 15; b=13-1=12. chegamos a uma diferença igual a 3. passo

3) 15^2 - 12^2 = 27x3 =81 = 9^2 . Então 15^2 = 12^2 + 9^2.

Temos aí o nosso Terno Pitagórico.

Abraço, Fernando Manso"

E-mail - data: 27/07/205

"Olá Ricardo, bom dia!

Em relação ao e-mail anterior.

Uma outra estratégia para encontrar a e b é utilizar as fórmulas:

a = [n^3 + n] / 2;

b = [n^3 - n] / 2.

No exemplo 3^3 . n

temos:

a = ( 27 + 3 ) / 2 = 15

e

b = ( 27 - 3 ) / 2 = 12.

27 x 3 = 81 = 9^ 2 = 15^2 - 12^2.

Portanto, 15^2 = 12^2 + 9^2.

Abraço, Fernando Manso."

Numeros Naturais elevados ao expoente 2

Utilizando-se o Método de Potências com expoente 2, são gerados ternos pitagóricos com as seguintes características e propriedades:

a) os catetos menores são números cúbicos perfeitos quando n é um quadrado perfeito;

b) o cateto maior e hipotenusa são números triangulares consecutivos;

c) a soma do cateto maior com a hipotenusa é um número quadrado perfeito e a raiz quadrada de n;

d) a soma do cateto maior com a hipotenusa é divisível pelo cateto menor;

c) a diferença entre a hipotenusa e o cateto maior é n.

Tabela 1
 
Fórmulas de Potências com expoente 2
               
          Terno
        raiz cateto cateto hipotenusa
        de menor maior  
n (n^2+n) / 2 (n^2-n) / 2 n^2 x n n^2 x n b c a
               
1 1 0 1 1      
2 3 1 8 2,828427 2,828427 1 3
3 6 3 27 5,196152 5,196152 3 6
4 10 6 64 8 8 6 10
5 15 10 125 11,18034 11,18034 10 15
6 21 15 216 14,69694 14,69694 15 21
7 28 21 343 18,52026 18,52026 21 28
8 36 28 512 22,62742 22,62742 28 36
9 45 36 729 27 27 36 45
10 55 45 1000 31,62278 31,62278 45 55
11 66 55 1331 36,48287 36,48287 55 66
12 78 66 1728 41,56922 41,56922 66 78
13 91 78 2197 46,87217 46,87217 78 91
14 105 91 2744 52,3832 52,3832 91 105
15 120 105 3375 58,09475 58,09475 105 120
16 136 120 4096 64 64 120 136
17 153 136 4913 70,0928 70,0928 136 153
18 171 153 5832 76,36753 76,36753 153 171
19 190 171 6859 82,81908 82,81908 171 190
20 210 190 8000 89,44272 89,44272 190 210
               
www.osfantasticosnumerosprimos.com.br

Numeros Naturais elevados ao expoente 3

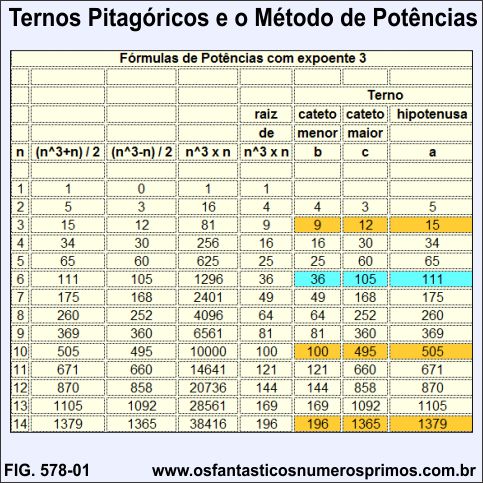
Utilizando-se o Método de Potências com expoente 3, são gerados ternos pitagóricos com as seguintes características e propriedades:

a) os catetos menores são números quadrados perfeitos;

b) a soma do cateto maior com a hipotenusa é o cubo de n;

c) a soma do cateto maior com a hipoteusa é divisível pelo cateto menor;

d) a diferença entre a hipotenusa e cateto maior é n;

e) as fórmulas geram o famoso Terno Pitagórico Primitivo 3-4-5;

f) os ternos nas células laranja não são gerados pelas Fórmulas de Euclides;

g) as fórmulas geram ternos pitagóricos cujos catetos menores são números triangulares quadrados perfeitos (células azuis).

36 e 1225 são números triangulares quadrados perfeitos.

Tabela 2
 
Fórmulas de Potências com expoente 3
               
          Terno
        raiz cateto cateto hipotenusa
        de menor maior  
n (n^3+n) / 2 (n^3-n) / 2 n^3 x n n^3 x n b c a
               
1 1 0 1 1      
2 5 3 16 4 4 3 5
3 15 12 81 9 9 12 15
4 34 30 256 16 16 30 34
5 65 60 625 25 25 60 65
6 111 105 1296 36 36 105 111
7 175 168 2401 49 49 168 175
8 260 252 4096 64 64 252 260
9 369 360 6561 81 81 360 369
10 505 495 10000 100 100 495 505
11 671 660 14641 121 121 660 671
12 870 858 20736 144 144 858 870
13 1105 1092 28561 169 169 1092 1105
14 1379 1365 38416 196 196 1365 1379
15 1695 1680 50625 225 225 1680 1695
16 2056 2040 65536 256 256 2040 2056
17 2465 2448 83521 289 289 2448 2465
18 2925 2907 104976 324 324 2907 2925
19 3439 3420 130321 361 361 3420 3439
20 4010 3990 160000 400 400 3990 4010
..              
35 21455 21420 1500625 1225 1225 21420 21455
               
www.osfantasticosnumerosprimos.com.br

Numeros Naturais elevados ao expoente 4

Utilizando-se o Método de Potências com expoente 4, são gerados ternos pitagóricos com as seguintes características e propriedades:

a) os catetos menores são números de quinta potência perfeitas quando n é quadrado perfeito;

b) a soma do cateto maior com a hipotenusa é um número quadrado perfeito do quadrado de n;

Exemplo:

4 130 126 1024 32 32 126 130

4 x 4 = 16

16 x 16 = 256

c) a soma do cateto maior com a hipotenusa é divisível pelo cateto menor;

c) a diferença entre hipotenusa e cateto maior é n.

Tabela 3
 
Fórmulas de Potências com expoente 4
 
          Terno
        raiz cateto cateto hipotenusa
        de menor maior  
n (n^4+n) / 2 (n^4-n) / 2 n^4 x n n^4 x n b c a
               
1 1 0 1 1      
2 9 7 32 5,656854 5,656854 7 9
3 42 39 243 15,58846 15,58846 39 42
4 130 126 1024 32 32 126 130
5 315 310 3125 55,9017 55,9017 310 315
6 651 645 7776 88,18163 88,18163 645 651
7 1204 1197 16807 129,6418 129,6418 1197 1204
8 2052 2044 32768 181,0193 181,0193 2044 2052
9 3285 3276 59049 243 243 3276 3285
10 5005 4995 100000 316,2278 316,2278 4995 5005
11 7326 7315 161051 401,3116 401,3116 7315 7326
12 10374 10362 248832 498,8306 498,8306 10362 10374
13 14287 14274 371293 609,3382 609,3382 14274 14287
14 19215 19201 537824 733,3648 733,3648 19201 19215
15 25320 25305 759375 871,4213 871,4213 25305 25320
16 32776 32760 1048576 1024 1024 32760 32776
17 41769 41752 1419857 1191,578 1191,578 41752 41769
18 52497 52479 1889568 1374,616 1374,616 52479 52497
19 65170 65151 2476099 1573,563 1573,563 65151 65170
20 80010 79990 3200000 1788,854 1788,854 79990 80010
               
www.osfantasticosnumerosprimos.com.br

Numeros Naturais elevados ao expoente 5

Utilizando-se o Método de Potências com expoente 5, são gerados ternos pitagóricos com as seguintes características e propriedades:

a) os catetos menores são números cúbicos;

b) a soma do cateto maior com a hipotenusa é um número de quinta potência de n;

c) a diferença entre hipotenusa e cateto maior é n.

Tabela 4
 
Fórmulas de Potências com expoente 5
               
          Terno
        raiz cateto cateto hipotenusa
        de menor maior  
n (n^5+n) / 2 (n^5-n) / 2 n^5 x n n^5 x n b c a
               
1 1 0 1 1      
2 17 15 64 8 8 15 17
3 123 120 729 27 27 120 123
4 514 510 4096 64 64 510 514
5 1565 1560 15625 125 125 1560 1565
6 3891 3885 46656 216 216 3885 3891
7 8407 8400 117649 343 343 8400 8407
8 16388 16380 262144 512 512 16380 16388
9 29529 29520 531441 729 729 29520 29529
10 50005 49995 1000000 1000 1000 49995 50005
11 80531 80520 1771561 1331 1331 80520 80531
12 124422 124410 2985984 1728 1728 124410 124422
13 185653 185640 4826809 2197 2197 185640 185653
14 268919 268905 7529536 2744 2744 268905 268919
15 379695 379680 11390625 3375 3375 379680 379695
16 524296 524280 16777216 4096 4096 524280 524296
17 709937 709920 24137569 4913 4913 709920 709937
18 944793 944775 34012224 5832 5832 944775 944793
19 1238059 1238040 47045881 6859 6859 1238040 1238059
20 1600010 1599990 64000000 8000 8000 1599990 1600010
               
www.osfantasticosnumerosprimos.com.br

Numeros Naturais elevados ao expoente 6

Utilizando-se o Método de Potências com expoente 6, são gerados ternos pitagóricos com as seguintes características e propriedades:

a) os catetos menores são números de sétima potência perfeitas quando n é quadrado perfeito;

b) a soma do cateto maior com a hipotenusa é um número de décima segunda potência da raiz quadrada de n.

Tabela 5
 
Fórmulas de Potências com expoente 6
               
          Terno
        raiz cateto cateto hipote-
        de menor maior nusa
n (n^6+n) / 2 (n^6-n) / 2 n^6 x n n^6 x n b c a
               
1 1 0 1 1      
2 33 31 128 11,31 11,31 31 33
3 366 363 2187 46,76 46,76 363 366
4 2050 2046 16384 128 128 2046 2050
5 7815 7810 78125 279,50 279,50 7810 7815
6 23331 23325 279936 529,08 529,08 23325 23331
7 58828 58821 823543 907,49 907,49 58821 58828
8 131076 131068 2097152 1448,15 1448,15 131068 131076
9 265725 265716 4782969 2187 2187 265716 265725
10 500005 499995 10000000 3162,2 3162,2 499995 500005
11 885786 885775 19487171 4414,4 4414,4 885775 885786
12 1492998 1492986 35831808 5985,9 5985,9 1492986 1492998
13 2413411 2413398 62748517 7921,3 7921,3 2413398 2413411
14 3764775 3764761 105413504 10267,1 10267,1 3764761 3764775
15 5695320 5695305 170859375 13071,3 13071,3 5695305 5695320
16 8388616 8388600 268435456 16384 16384 8388600 8388616
17 12068793 12068776 410338673 20256,8 20256,8 12068776 12068793
18 17006121 17006103 612220032 24743,0 24743,0 17006103 17006121
19 23522950 23522931 893871739 29897,6 29897,6 23522931 23522950
20 32000010 31999990 1280000000 35777,0 35777,0 31999990 32000010
               
www.osfantasticosnumerosprimos.com.br

Numeros Naturais elevados ao expoente 7

Utilizando-se o Método de Potências com expoente 7, são gerados ternos pitagóricos com as seguintes características e propriedades:

a) os catetos menores são números quadrados do dobro de n;

b) a soma da hipotenusa com o cateto maior é divisível pelo cateto menor;

c) a soma da hipotenusa com o cateto maior é uma potência de n;

Tabela 6
 
Fórmulas de Potências com expoente 7
               
          Terno
        raiz cateto cateto hipote-
        de menor maior nusa
n (n^7+n) / 2 (n^7-n) / 2 n^7 x n n^7 x n b c a
               
1 1 0 1 1      
2 65 63 256 16 16 63 65
3 1095 1092 6561 81 81 1092 1095
4 8194 8190 65536 256 256 8190 8194
5 39065 39060 390625 625 625 39060 39065
6 139971 139965 1679616 1296 1296 139965 139971
7 411775 411768 5764801 2401 2401 411768 411775
8 1048580 1048572 16777216 4096 4096 1048572 1048580
9 2391489 2391480 43046721 6561 6561 2391480 2391489
10 5000005 4999995 100000000 10000 10000 4999995 5000005
11 9743591 9743580 214358881 14641 14641 9743580 9743591
12 17915910 17915898 429981696 20736 20736 17915898 17915910
13 31374265 31374252 815730721 28561 28561 31374252 31374265
14 52706759 52706745 1475789056 38416 38416 52706745 52706759
15 85429695 85429680 2562890625 50625 50625 85429680 85429695
16 134217736 134217720 4294967296 65536 65536 134217720 1,34E+08
17 205169345 205169328 6975757441 83521 83521 205169328 2,05E+08
18 306110025 306110007 11019960576 104976 104976 306110007 3,06E+08
19 446935879 446935860 16983563041 130321 130321 446935860 4,47E+08
20 640000010 639999990 25600000000 160000 160000 639999990 6,4E+08
               
www.osfantasticosnumerosprimos.com.br

Numeros Naturais elevados ao expoente 11

Utilizando-se o Método de Potências com expoente 11, são gerados ternos pitagóricos com as seguintes características e propriedades:

a) os catetos menores são formados por números quadrado cúbicos.

Exemplo:

64 é o quadrado do cubo 8 ( 8 x 8 = 64)

64 é o cubo do quadrado 4 ( 4 x 4 x 4 = 64)

Para mais informações, veja:

011-estudos-577-numeros-quadrados-cubicos

Tabela 7
               
Fórmulas de Potências com expoente 11
               
            Terno  
          cateto cateto hipote-
        raiz de menor maior nusa
n (n^11+n) / 2 (n^11-n) / 2 n^11 x n n^11 x n b c a
               
1 1 0 1 1      
2 1025 1023 4096 64 64 1023 1025
3 88575 88572 531441 729 729 88572 88575
4 2097154 2097150 16777216 4096 4096 2097150 2097154
5 24414065 24414060 244140625 15625 15625 24414060 24414065
6 181398531 181398525 2176782336 46656 46656 181398525 181398531
7 988663375 988663368 13841287201 117649 117649 988663368 988663375
8 4294967300 4294967292 68719476736 262144 262144 4294967292 4294967300
9 15690529809 1,5691E+10 2,8243E+11 531441 531441 1,5691E+10 15690529809
10 50000000005 5E+10 1E+12 1000000 1000000 5E+10 50000000005
11 1,42656E+11 1,4266E+11 3,13843E+12 1771561 1771561 1,4266E+11 1,42656E+11
12 3,71504E+11 3,715E+11 8,9161E+12 2985984 2985984 3,715E+11 3,71504E+11
13 8,9608E+11 8,9608E+11 2,32981E+13 4826809 4826809 8,9608E+11 8,9608E+11
14 2,02478E+12 2,0248E+12 5,66939E+13 7529536 7529536 2,0248E+12 2,02478E+12
15 4,32488E+12 4,3249E+12 1,29746E+14 11390625 11390625 4,3249E+12 4,32488E+12
16 8,79609E+12 8,7961E+12 2,81475E+14 16777216 16777216 8,7961E+12 8,79609E+12
17 1,71359E+13 1,7136E+13 5,82622E+14 24137569 24137569 1,7136E+13 1,71359E+13
18 3,21342E+13 3,2134E+13 1,15683E+15 34012224 34012224 3,2134E+13 3,21342E+13
19 5,82451E+13 5,8245E+13 2,21331E+15 47045881 47045881 5,8245E+13 5,82451E+13
20 1,024E+14 1,024E+14 4,096E+15 64000000 64000000 1,024E+14 1,024E+14
               
www.osfantasticosnumerosprimos.com.br

Números de Mersenne (números quase potências de base 2)

Montando-se a Tabela 8 somente com as segundas linhas das tabela de 1 a 6, isto é, onde n é igual 2, verifica-se que:

a) a diferença entre hipotenusa e cateto maior são de 2 unidades;

b) os catetos menores são termos da sequência de Números de Mersenne:, 1, 3, 7, 15,... (números quase potências de base 2);

c) as hipotenusas são termos da sequência de números ímpares que são 1 unidade maior que uma potência de base 2 e, entre os termos, Números de Fermat: 3, 5, 17;

d) a soma de cada dupla de números ímpares têm como resultado potência de base 2;

e) a média aritmética de cada dupla de números ímpares é uma potência de base 2.

Interessante observar que produtos de Números de Mersenne por Números de Fermat resultam em Números de Mersenne (números quase potências de base 2).

Exemplos:

1 x 3 = 3

3 x 5 = 15

15 x 17 = 255

Tabela 8
               
          Terno
        raiz      
        de cateto cateto hipote-
n (n^z+n) / 2 (n^z-n) / 2 n^z x n n^z x n menor maior nusa
          b c a
               
            Números Números
            Mersenne Fermat
               
               
2 3 1 8 2,828427 2,828427 1 3
               
2 5 3 16 4 4 3 5
               
2 9 7 32 5,656854 5,656854 7 9
               
2 17 15 64 8 8 15 17
               
2 33 31 128 11,3137085 11,3137085 31 33
               
2 65 63 256 16 16 63 65
               
www.osfantasticosnumerosprimos.com.br

Conclusão:

Quando nas Fórmulas os expoentes são ímpares, todos o resultados são números inteiros.

Quando nas Fórmulas os expoentes são pares, os resultados apresentam números inteiros e números decimais somente nos catetos menores.

Diferentemente de outros métodos, que necessitam de 2 números naturais (dois termos) para se gerar cada terno pitagórico, no Método de Potências, precisa-se de um só número (diferente) para se gerar cada terno pitagórico.

Autor: Ricardo Silva - julho/2025

Fontes Bibliográficas:

NASCIMENTO, Sebastião Vieira. Desvendando os segredos do triângulo retângulo e descobrindo curisosidades até hoje não conhecidas. / Sebastião Vieira do Nascimento. - Rio de Janeiro: Gramma, 2018

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020

SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022

SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Matérias relacionadas:

011-estudos-069-ternos-pitagoricos
011-estudos-070-ternos-pitagoricos-angulos-triangulos-retangulos
011-estudos-141-numeros-mersenne-e-numeros-binarios
011-estudos-443-numeros-triangulares-quadrados-perfeitos
011-estudos-522-numeros-fermat-regularidades-numericas
011-estudos-577-numeros-quadrados-cubicos
Livro digital (e-book)
Escada de Theon
e Sequências Numéricas
Escada de Theon e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Primos e o
Método Números Atraentes
livro Números Primos e o Método Números Atraentes

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Progressões Aritméticas e Geométricas
livro digital Progressões Aritméticas e Geometricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Tabuada de Pythagoras
e Sequências Numéricas
livro digital Tabuada de Pythagoras e sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Estudos de Sequências Numéricas
livro estudos de sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Os Fantásticos Números Primos
livro os fantasticos números primos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Ternos Pitagóricos e Sequências Numéricas
livro Ternos Pitagóricos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

Recebam GRATUITAMENTE
o E-book
Triângulo Retângulo

 

livro Triângulo Retângulo

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Livro Digital (e-book) Descobrindo Números Primos a partir de Números Compostos
livro descobrindo numeros primos a partir numeros compostos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (E-book) Quadrados Mágicos e Sequências Numéricas
livro quadrados mágicos e sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Triangulares e Sequências Numéricas
livro triangulares e sequências numéricas mágicas

Mais informações, acesse:

SEÇÃO LIVROS

Manual digital (E-book) Quadrado Mágico Triplo
livro quadrado mágico triplo
LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Perfeitos e Sequências Numéricas
livro Números Perfeitos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Multiplicação através da soma de múltiplos
livro multiplicação através da soma de múltiplos
LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.

curta fantasticos numeros primos no facebook
anúncio dominó tri-minox anúncio dominó quadriminox
logotipo Ric Desing

Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.

Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).

Desenvolvimento de WebSite.

Contato

ric@osfantasticosnumerosprimos.com.br

fapage dos fantasticos numeros primos
Canal youtube dos fantasticos numeros primos