


Número Perfeito é um número cuja soma de seu divisores próprios, excluindo o próprio número, têm como resultado esse mesmo número.
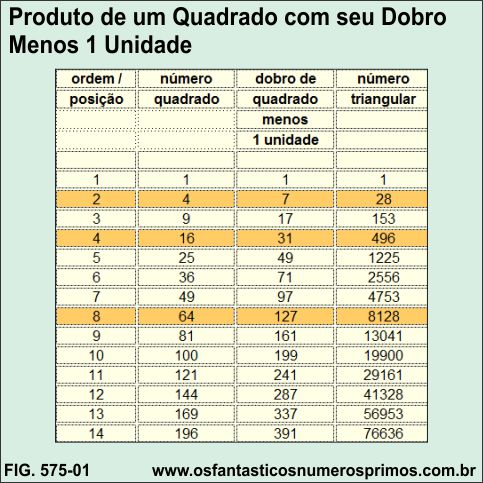
O presente estudo demonstram que produtos de um número quadrado perfeito com seu dobro menos 1 unidade têm como resultados números triangulares cujas ordens / posições são ímpares.
Entre os números triangulares, há ocorrências de números perfeitos, bem como, números triangulares quadrados perfeitos.
Euclides em Os Elementos, Livro IX, demonstra que duplicando-se a unidade (número 1) até que se encontre um número primo, e este primo multiplicado pela última soma, então o produto é um número perfeito.
A sequência a que Euclides se refere em Os Elementos são as potências de base 2.
1
1 + 2 = 3 (número primo)
(3 x 2 = 6)
1 + 2 + 4 = 7 (número primo)
(7 x 4 = 28)
1 + 2 + 4 + 8 = 15 (não é número primo)
1 + 2 + 4 + 8 + 16 = 31 (número primo)
(31 x 16 = 496)
| 2n - 1(2n - 1) |
para n = 2:
22 - 1 (22 − 1) = 6
para n = 3:
23 - 1 (23 − 1) = 28
para n = 5:
25 - 1(25 − 1) = 496
para n = 7:
27 - 1 (27 − 1) = 8.128
Marin Mersenne (1588-1648), matemático, teórico musical, padre mínimo, teólogo e filósofo francês, também estudou os números perfeitos apresentado a seguinte fórmula:
| 2n - 1 |
onde uma potência de base 2 elevada a um número natural e subtraindo uma unidade gera um número antecessor de número quase perfeito.
Números gerados pela Fórmula de Mersenne, são chamados de Primos de Mersenne, mas nem todos os números gerados são primos, há números compostos também.
Número Primo de Mersenne multiplicado pelo seu sucessor e posteriormente dividido por 2 é um número perfeito, o mesmo que:
O produto de 2 números consecutivos divididos por 2 tem como resultado um número triangular.
A Fórmula de Mersenne também pode ser representada da seguinte forma: base 2 elevada a um expoente primo subtraída 1 unidade.
| 2p - 1 |
Lembrando que mesmo a base 2 elevada a um expoente primo e subtraída 1 unidade, nem sempre, o resultado será um número primo, aliás, o WebSite:
https://www.mersenne.org/
utiliza a imagem de Marin Mersenne com a fórmula acima e com o seguinte slogan:
2p - 1 May Be Prime!
Exemplos:
3 x 4 = 12
12 : 2 = 6 (número perfeito)
7 x 8 = 56
56 : 2 = 28 (número perfeito)
A Tabela 1 a seguir também se encontra publicada no estudo:
011-estudos-574-numeros-triangulares-quadrados-gerados-dois-quadrados-nao-consecutivos
e sua contrução se dá com as seguintes etapas:
a) coluna A é a ordem / posição de cada multiplicação;
b) coluna B formada por números quadrados perfeitos;
c) coluna C formada por dobros da coluna B menos 1 unidade;
d) coluna D formada por produtos da coluna B com C;
e) coluna E formanda por raízes quadradas da coluna D.
a apresenta a seguintes propriedades:
| Tabela 1 | ||||
| Quadrado multiplicado | ||||
| por | ||||
| Quadrado menso 1 unidade | ||||
| A | B | C | D | E |
| ordem / | número | dobro de | número | raiz |
| posição | quadrado | quadrado | triangular | quadrada |
| menos | ||||
| 1 unidade | ||||
| 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 7 | 28 | 5,291502622 |
| 3 | 9 | 17 | 153 | 12,36931688 |
| 4 | 16 | 31 | 496 | 22,27105745 |
| 5 | 25 | 49 | 1225 | 35 |
| 6 | 36 | 71 | 2556 | 50,55689864 |
| 7 | 49 | 97 | 4753 | 68,94200461 |
| 8 | 64 | 127 | 8128 | 90,15542136 |
| 9 | 81 | 161 | 13041 | 114,1971979 |
| 10 | 100 | 199 | 19900 | 141,0673598 |
| 11 | 121 | 241 | 29161 | 170,7659217 |
| 12 | 144 | 287 | 41328 | 203,2928922 |
| 13 | 169 | 337 | 56953 | 238,6482768 |
| 14 | 196 | 391 | 76636 | 276,8320791 |
| 15 | 225 | 449 | 101025 | 317,8443015 |
| 16 | 256 | 511 | 130816 | 361,6849458 |
| 17 | 289 | 577 | 166753 | 408,3540131 |
| 18 | 324 | 647 | 209628 | 457,8515043 |
| 19 | 361 | 721 | 260281 | 510,1774201 |
| 20 | 400 | 799 | 319600 | 565,331761 |
| 21 | 441 | 881 | 388521 | 623,3145273 |
| 22 | 484 | 967 | 468028 | 684,1257194 |
| 23 | 529 | 1057 | 559153 | 747,7653375 |
| 24 | 576 | 1151 | 662976 | 814,2333818 |
| 25 | 625 | 1249 | 780625 | 883,5298524 |
| 26 | 676 | 1351 | 913276 | 955,6547494 |
| 27 | 729 | 1457 | 1062153 | 1030,608073 |
| 28 | 784 | 1567 | 1228528 | 1108,389823 |
| 29 | 841 | 1681 | 1413721 | 1189 |
| 30 | 900 | 1799 | 1619100 | 1272,438604 |
| 31 | 961 | 1921 | 1846081 | 1358,705634 |
| 32 | 1024 | 2047 | 2096128 | 1447,801091 |
| 33 | 1089 | 2177 | 2370753 | 1539,724975 |
| 34 | 1156 | 2311 | 2671516 | 1634,477286 |
| 35 | 1225 | 2449 | 3000025 | 1732,058024 |
| 36 | 1296 | 2591 | 3357936 | 1832,467189 |
| 37 | 1369 | 2737 | 3746953 | 1935,704781 |
| 38 | 1444 | 2887 | 4168828 | 2041,7708 |
| 39 | 1521 | 3041 | 4625361 | 2150,665246 |
| 40 | 1600 | 3199 | 5118400 | 2262,388119 |
| 41 | 1681 | 3361 | 5649841 | 2376,939419 |
| 42 | 1764 | 3527 | 6221628 | 2494,319146 |
| 43 | 1849 | 3697 | 6835753 | 2614,5273 |
| 44 | 1936 | 3871 | 7494256 | 2737,563881 |
| 45 | 2025 | 4049 | 8199225 | 2863,428889 |
| 46 | 2116 | 4231 | 8952796 | 2992,122324 |
| 47 | 2209 | 4417 | 9757153 | 3123,644186 |
| 48 | 2304 | 4607 | 10614528 | 3257,994475 |
| 49 | 2401 | 4801 | 11527201 | 3395,173191 |
| 50 | 2500 | 4999 | 12497500 | 3535,180335 |
| 51 | 2601 | 5201 | 13527801 | 3678,015905 |
| 52 | 2704 | 5407 | 14620528 | 3823,679903 |
| 53 | 2809 | 5617 | 15778153 | 3972,172328 |
| 54 | 2916 | 5831 | 17003196 | 4123,493179 |
| 55 | 3025 | 6049 | 18298225 | 4277,642458 |
| 56 | 3136 | 6271 | 19665856 | 4434,620164 |
| 57 | 3249 | 6497 | 21108753 | 4594,426297 |
| 58 | 3364 | 6727 | 22629628 | 4757,060857 |
| 59 | 3481 | 6961 | 24231241 | 4922,523845 |
| 60 | 3600 | 7199 | 25916400 | 5090,815259 |
| 61 | 3721 | 7441 | 27687961 | 5261,9351 |
| 62 | 3844 | 7687 | 29548828 | 5435,883369 |
| 63 | 3969 | 7937 | 31501953 | 5612,660065 |
| 64 | 4096 | 8191 | 33550336 | 5792,265187 |
| www.osfantasticosnumerosprimos.com.br | ||||
f) potências de base 2 que são quadrados perfeitos multiplicadas pelos seus dobros menos 1 unidade têm como produtos números triangulares e, entre eles, números perfeitos;
Observação Importante: os números triangulares gerados na tabela acima são todos números triangulares de ordens / posições ímpares.
As ordens / posicões ímpares dos números triangulares são os próprios dobros dos quadrados menos 1 unidade na coluna C.
Exemplos:
| ordem / | número | dobro de | número | raiz |
| posição | quadrado | quadrado | triangular | quadrada |
| menos | ||||
| 1unidade | ||||
| 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 7 | 28 | 5,291502622 |
| www.osfantasticosnumerosprimos.com.br | ||||
28 é um número perfeito.
28 é sétimo número triangular e perfeito.
| ordem / | número | dobro de | número | raiz |
| posição | quadrado | quadrado | triangular | quadrada |
| menos | ||||
| 1unidade | ||||
| 4 | 16 | 31 | 496 | 22,27105745 |
| www.osfantasticosnumerosprimos.com.br | ||||
496 é um número perfeito.
496 é trigésimo primeiro número triangular e perfeito.
| ordem / | número | dobro de | número | raiz |
| posição | quadrado | quadrado | triangular | quadrada |
| menos | ||||
| 1unidade | ||||
| 8 | 64 | 127 | 8128 | 90,15542136 |
| www.osfantasticosnumerosprimos.com.br | ||||
8128 é um número perfeito.
8128 é centésimo vigésimo sétimo número triangular e perfeito.
de onde se deduz a seguinte fórmula:
| 2^2n - 2 x [ ( 2 x 2^2n - 2 ) - 1 ] |
para n igual ou maior que 2, com ocorrências de números perfeitos.
A base 2 está sendo elevada a expoente par para se gerar quadrado perfeito.
2^2 x ( 2 x 2^2 - 1 )
4 x ( 2 x 4 - 1 )
4 x 7 = 28
O segundo fator 7 é 1 unidade menor do dobro do quadrado 4 e também a ordem / posição original do número triangular 28.
2^4 x ( 2 x 2^4 - 1 )
16 x ( 2 x 16 - 1 )
16 x 31 = 496
O segundo fator 31 é 1 unidade menor do dobro do quadrado 16 e também a ordem / posição original do número triangular 496.
2^6 x ( 2 x 2^6 - 1 )
64 x ( 2 x 64 - 1 )
64 x 127 = 8128
O segundo fator 127 é 1 unidade menor do dobro do quadrado 64 e também a ordem / posição original do número triangular 8128.
A Tabela 2 foi gerada da Tabela 1 acima preservando as coluna C e D.
A coluna C são são ordens / posições originais dos respectivos números triangulares da coluna D.
Efetuando-se subtrações de um número triangular sucessor por um triangular antecessor, têm-se como diferenças a sequência de números cúbicos perfeitos de ordens / posições ímpares.
| Tabela 2 | ||||
| Números Triangulares | ||||
| de ordens / posições ímpares | ||||
| C | D | F | ||
| ordem / | número | diferença | ||
| posição | triangular | número | ||
| original | cúbico | |||
| perfeito | ||||
| 1 | 1 | |||
| 27 | = | 33 | ||
| 7 | 28 | |||
| 125 | = | 53 | ||
| 17 | 153 | |||
| 343 | = | 73 | ||
| 31 | 496 | |||
| 729 | = | 93 | ||
| 49 | 1225 | |||
| 1331 | = | 113 | ||
| 71 | 2556 | |||
| 2197 | = | 133 | ||
| 97 | 4753 | |||
| 3375 | = | 153 | ||
| 127 | 8128 | |||
| 4913 | = | 173 | ||
| 161 | 13041 | |||
| 6859 | = | 193 | ||
| 199 | 19900 | |||
| 9261 | = | 213 | ||
| 241 | 29161 | |||
| 12167 | = | 233 | ||
| 287 | 41328 | |||
| 15625 | = | 253 | ||
| 337 | 56953 | |||
| 19683 | = | 273 | ||
| 391 | 76636 | |||
| 24389 | = | 293 | ||
| 449 | 101025 | |||
| 29791 | = | 313 | ||
| 511 | 130816 | |||
| www.osfantasticosnumerosprimos.com.br | ||||
A soma de números cúbicos consecutivos têm como resultados números quadrados pefeitos cujas raízes quadradas são números triagulares:
1 + 8 = 9
raiz de 9 é 3 (3 é um número triangular)
1 + 8 + 27 = 36
raiz de 36 é 6 (6 é um número triangular)
1 + 8 + 27 + 64 = 100
raiz de 100 é 10 (10 é um número triangular)
A soma de números cúbicos consecutivos de ordens / posições ímpares têm como resultados números triangulares também de ordens / posições ímpares e, entre eles, números triangulares perfeitos e números triangulares quadrados perfeitos.
Interessante observar que as ordens / posições de números perfeitos são Números de Mersenne (números 1 unidade menor de uma potência de base 2).
Observação: conforme pesquisas realizadas sobre o assunto, esta propriedade relacionada a números cúbicos com números triangulares perfeitos e triangulares quadrados é inédita, pois até o presente momento, não se tem conhecimento se já fora publicada.
| Tabela 3 | |||
| Soma de Números Cúbicos Consecutivos | |||
| de ordens / posições ímpares | |||
| ordem / | número | soma de | número |
| posição | cúbico | números | |
| ímpar | cúbicos | ||
| 1 | 1 | ||
| 3 | 27 | 28 | perfeito |
| 5 | 125 | 153 | |
| 7 | 343 | 496 | perfeito |
| 9 | 729 | 1225 | triangular quadrado |
| 11 | 1331 | 2556 | |
| 13 | 2197 | 4753 | |
| 15 | 3375 | 8128 | perfeito |
| 17 | 4913 | 13041 | |
| 19 | 6859 | 19900 | |
| 21 | 9261 | 29161 | |
| 23 | 12167 | 41328 | |
| 25 | 15625 | 56953 | |
| 27 | 19683 | 76636 | |
| 29 | 24389 | 101025 | |
| 31 | 29791 | 130816 | |
| 33 | 35937 | 166753 | |
| 35 | 42875 | 209628 | |
| 37 | 50653 | 260281 | |
| 39 | 59319 | 319600 | |
| 41 | 68921 | 388521 | |
| 43 | 79507 | 468028 | |
| 45 | 91125 | 559153 | |
| 47 | 103823 | 662976 | |
| 49 | 117649 | 780625 | |
| 51 | 132651 | 913276 | |
| 53 | 148877 | 1062153 | |
| 55 | 166375 | 1228528 | |
| 57 | 185193 | 1413721 | triangular quadrado |
| 59 | 205379 | 1619100 | |
| 61 | 226981 | 1846081 | |
| 63 | 250047 | 2096128 | |
| 65 | 274625 | 2370753 | |
| 67 | 300763 | 2671516 | |
| 69 | 328509 | 3000025 | |
| 71 | 357911 | 3357936 | |
| 73 | 389017 | 3746953 | |
| 75 | 421875 | 4168828 | |
| 77 | 456533 | 4625361 | |
| 79 | 493039 | 5118400 | |
| 81 | 531441 | 5649841 | |
| 83 | 571787 | 6221628 | |
| 85 | 614125 | 6835753 | |
| 87 | 658503 | 7494256 | |
| 89 | 704969 | 8199225 | |
| 91 | 753571 | 8952796 | |
| 93 | 804357 | 9757153 | |
| 95 | 857375 | 10614528 | |
| 97 | 912673 | 11527201 | |
| 99 | 970299 | 12497500 | |
| 101 | 1030301 | 13527801 | |
| 103 | 1092727 | 14620528 | |
| 105 | 1157625 | 15778153 | |
| 107 | 1225043 | 17003196 | |
| 109 | 1295029 | 18298225 | |
| 111 | 1367631 | 19665856 | |
| 113 | 1442897 | 21108753 | |
| 115 | 1520875 | 22629628 | |
| 117 | 1601613 | 24231241 | |
| 119 | 1685159 | 25916400 | |
| 121 | 1771561 | 27687961 | |
| 123 | 1860867 | 29548828 | |
| 125 | 1953125 | 31501953 | |
| 127 | 2048383 | 33550336 | perfeito |
| www.osfantasticosnumerosprimos.com.br | |||
Autor: Ricardo Silva - julho/2025
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato