capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

A soma de dois números quadrados perfeitos pares consecutivos - 360

A diferença entre dois números quadrados perfeitos consecutivos apresentam duas importantes regularidades numéricas:

a) geram a sequência de números ímpares a partir do número 3 e

b) geram a sequência de números quadrados perfeitos ímpares a partir do quadrado 9.

Soma de 2 números quadrados perfeitos pares consecutivos

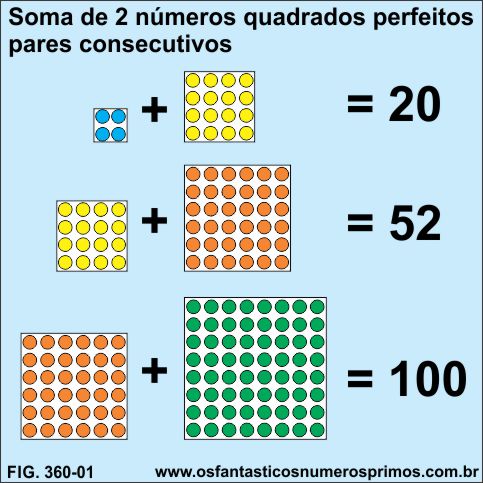
Diferentemente, a soma de dois números quadrados perfeitos pares consecutivos geram sequências aleatórias de números quadrados perfeitos, isto porque, num rol dos 2.000 primeiros números pares consecutivos elevados ao quadrado e somados com seus respectivos quadrados consecutivos encontramos somente 4 ternos pitagóricos derivados os quais também podem ser gerados pelas Fórmulas de Euclides.

Terno pitagórico derivado 6-8-10

Posição/	Número	Número	Número	Soma 2
ordem	par	Quadrado	Quadrado	quadrados

3	6	36	64	100
4	8	64

√100 = 10

Terno pitagórico derivado 40-42-58

Posição/	Número	Número	Número	Soma 2
ordem	par	Quadrado	Quadrado	quadrados

20	40	1.600	1.764	3.364
21	42	1.764

√3.364 = 58

Terno pitagórico derivado 238-240-338

Posição/	Número	Número	Número	Soma 2
ordem	par	Quadrado	Quadrado	quadrados

119	238	56.644	57.600	114.244
120	240	57.600

√114.244 = 338

Terno pitagórico derivado 1392-1394-1970

Posição/	Número	Número	Número	Soma 2
ordem	par	Quadrado	Quadrado	quadrados

696	1392	1.937.664	1.943.236	3.880.900
697	1394	1.943.236

√3.880.900 = 1.970

Tabela da soma de dois quadrados perfeitos pares

A tabela a seguir demonstra de forma sintetizada as 50 primeiras somas de dois números quadrados perfeitos pares consecutivos e entre as somas os dois primeiros ternos pitagóricos derivados: (6-8-10) e (40-42-58).

Tabela da soma
de dois números
quadrados pares consecutivos

posição/	número	números		soma 2	raiz
ordem	par	quadrados		quadrados	quadrada
				pares

1	2	4	16	20	4,47
2	4	16	36	52	7,21
3	6	36	64	100	10
4	8	64	100	164	12,81
5	10	100	144	244	15,62
6	12	144	196	340	18,44
7	14	196	256	452	21,26
8	16	256	324	580	24,08
9	18	324	400	724	26,91
10	20	400	484	884	29,73
11	22	484	576	1060	32,56
12	24	576	676	1252	35,38
13	26	676	784	1460	38,21
14	28	784	900	1684	41,04
15	30	900	1024	1924	43,86
16	32	1024	1156	2180	46,69
17	34	1156	1296	2452	49,52
18	36	1296	1444	2740	52,35
19	38	1444	1600	3044	55,17
20	40	1600	1764	3364	58
21	42	1764	1936	3700	60,83
22	44	1936	2116	4052	63,66
23	46	2116	2304	4420	66,48
24	48	2304	2500	4804	69,31
25	50	2500	2704	5204	72,14
26	52	2704	2916	5620	74,97
27	54	2916	3136	6052	77,79
28	56	3136	3364	6500	80,62
29	58	3364	3600	6964	83,45
30	60	3600	3844	7444	86,28
31	62	3844	4096	7940	89,11
32	64	4096	4356	8452	91,93
33	66	4356	4624	8980	94,76
34	68	4624	4900	9524	97,59
35	70	4900	5184	10084	100,42
36	72	5184	5476	10660	103,25
37	74	5476	5776	11252	106,08
38	76	5776	6084	11860	108,90
39	78	6084	6400	12484	111,73
40	80	6400	6724	13124	114,56
41	82	6724	7056	13780	117,39
42	84	7056	7396	14452	120,22
43	86	7396	7744	15140	123,04
44	88	7744	8100	15844	125,87
45	90	8100	8464	16564	128,70
46	92	8464	8836	17300	131,53
47	94	8836	9216	18052	134,36
48	96	9216	9604	18820	137,19
49	98	9604	10000	19604	140,01
50	100	10000	10404	20404	142,84

www.osfantasticosnumerosprimos.com.br

A soma de dois quadrados perfeitos pares e o número 5

Outras características numéricas constatadas nas soma de 2 números quadrados perfeitos pares consecutivos são:

a) que efetuando a divisão por 2, temos como resultados números ímpares com ocorrências constantes de múltiplos de 5 e ocorrências aleatórias de números primos;

b) que determinados múltiplos de 5 divididos pelo próprio 5 apresentam como resultados números primos;

c) que as somas são números da forma 4x + 1, números estes que ao serem divididos por 4 deixam resto 1;

d) números da forma 4x + 1 são números que podem ser escritos como soma de 2 quadrados;

Veja matérias relacionadas:

	Soma de 2
	números quadrados
	e divisão por 5

soma 2	primeira	segunda
quadrados	divisão	divisão
	por 2	por 2

20	10	5
52	26	13
100	50	25
164	82	41
244	122	61
340	170	85
452	226	113
580	290	145
724	362	181
884	442	221
1060	530	265
1252	626	313
1460	730	365
1684	842	421
1924	962	481
2180	1090	545
2452	1226	613
2740	1370	685
3044	1522	761
3364	1682	841
3700	1850	925
4052	2026	1013
4420	2210	1105
4804	2402	1201
5204	2602	1301
5620	2810	1405
6052	3026	1513
6500	3250	1625
6964	3482	1741
7444	3722	1861
7940	3970	1985
8452	4226	2113
8980	4490	2245
9524	4762	2381
10084	5042	2521
10660	5330	2665
11252	5626	2813
11860	5930	2965
12484	6242	3121
13124	6562	3281
13780	6890	3445
14452	7226	3613
15140	7570	3785
15844	7922	3961
16564	8282	4141
17300	8650	4325
18052	9026	4513

www.osfantasticosnumerosprimos.com.br