


Quadrados Mágicos são dispositivos numéricos, formados por células em quantidades de números quadrados perfeitos, nos quais:
a) dispondo sequências numéricas formadas por progressões aritméticas, em certa ordem, as somas de cada uma das linhas, cada uma das colunas, bem como, as diagonais tem como resultado um mesmo total, denominada de Constante Mágica;
b) dispondo sequências numéricas formadas por progressões geométricas ou determinados conjuntos de divisores de um número natural, em certa ordem, os produtos de cada uma das linhas, cada uma das colunas, bem como, as diagonais tem como resultado um mesmo produto, denominado de Contante Mágica.
Quadrado Mágico 4x4 ou de ordem 4 é um quadrado quadriculado formado por 4 linhas e 4 colunas perfazendo um total de 16 células.
O Quadrado Mágico de ordem 4, Normal ou Puro tem como formação os 16 primeiros números naturais (1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ,11, 12 , 13, 14, 15 e 16) ou 1 a n2.
O presente estudo têm por objetivo demonstrar características construtivas, propriedades numéricas, bem como, curiosidades relacionadas ao Quadrado Mágico 4x4 de Ramanujan.
Srinivāsa Aiyangār Rāmānujan (Erode, 22 de dezembro de 1887-Kumbakonam, 26 de abril de 1920) foi um matemático indiano. Sem qualquer formação acadêmica, deu contributos importantes para as áreas da análise matemática, teoria dos números, séries infinitas, frações continuadas, entre outros ramos da matemática, incluindo problemas considerados insolúveis.[1]
Um dos diferenciais, como outros, no Quadrado Mágico 4x4 de Ramanujan é que os quatro primeiros números na primeira linha (22, 12, 18, 87) são a data de nascimento do próprio Srinivasa Ramanujan (22 de dezembro de 1887).
Partindo de sua data de nascimento, Ramanujan, então construiu o quadrado mágico e que contêm outras curiosidades.

Construindo quadrado 4x4 com o Método Moschopoulus com as sequências numéricas do Quadrado Mágico 4x4 de Ramanujan, o quadrado formado não é quadrado mágico perfeito, pois duas linhas do quadrado formam constante mágica 82 e outras duas 196, diferentemente da constante mágica original que é 139.
Para mais informações, sobre o Método Moschopoulus de Construção de Quadrados Mágicos, veja abaixo, Matérias Relacionadas!

Partindo-se da data de nascimento de Ramanujan, pode-se conjecturar que as 4 sequências podem ter sidos formadas com no exemplo a seguir:
| 22 | 23 | 24 | 25 | |||
| 09 | 10 | 11 | 12 | |||
| 16 | 17 | 18 | 19 | |||
| 86 | 87 | 88 | 89 |
a) sequência 22, 23, 24 e 25, progressão aritmética de razão 1;
b) sequência 9, 10, 11 e 12, progressão aritmética de razão 1;
c) sequência 16, 17, 18 e 19, progressão aritmética de razão 1;
d) sequência 86, 87, 88 e 89, progressão aritmética de razão 1;
9, 10, 11 e 12,
diferença 4, isto é 16 - 12
16, 17, 18 e 19,
diferença 3, isto é 22 - 19
22, 23, 24 e 25,
diferença 61, isto é 86 - 25
86, 87, 88 e 89
As diferenças entre as sequências não formam constante.
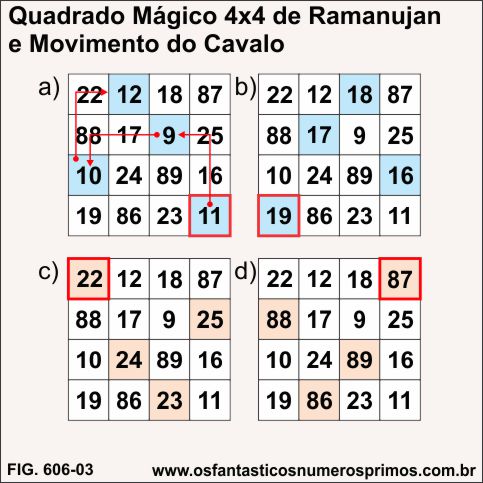
Destacando pares de sequências numéricas com cores azuis e laranjas, contata-se simetrias entre elas.
Pode-se conjecturar também que Ramanujan fez uso do movimento (da letra ELE) do Cavalo do Jogo de Xadrez, sempre iniciando os movimentos dos cantos do quadrado das seguintes formas:
a) do 11 para o 9, do 9 para o 10, do 10 para o 12;
b) do 19 para o 17, do 17 para o 16, do 16 para o 18;
c) do 22 para o 24, do 24 para o 25; 25 para o 23;
d) do 87 para o 89, do 89 para 88, 88 para 86.
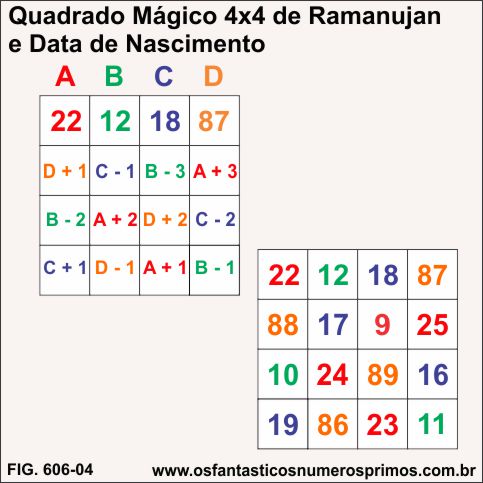
Um método bastante divulgado na Word Wide Web tendo como referência o Quadrado Mágico 4x4 de Ramanujan é representar a data de nascimento pela letras A, B, C e D e somar e subtrair algumas unidades e completar os restantes das células de forma obter outro quadrado mágico com outras sequências numéricas.
Quadrado mágico normal ou puro não pode haver repetições de números, mas não se pode dizer o mesmo de datas de nascimentos.
O WebSite Os Fantásticos Números Primos convida o Sr. Visitante a tentar a construir outro (s) quadrado(s) mágico(s) cujos números não se repetem a partir de data de nascimento acessando o desafio:
013-078-desafio-quadrado-magico-4x4-ramanujan
| A | B | C | D | |
| 4 | ||||
| 1 | 1 | 1 | 1 | 4 |
| 2 | 0 | -2 | 4 | 4 |
| -1 | 3 | 3 | -1 | 4 |
| 2 | 0 | 2 | 0 | 4 |
| 4 | 4 | 4 | 4 | 4 |
| A | B | C | D | |
| 44 | ||||
| 11 | 11 | 11 | 11 | 44 |
| 12 | 10 | 8 | 14 | 44 |
| 9 | 13 | 13 | 9 | 44 |
| 12 | 10 | 12 | 10 | 44 |
| 44 | 44 | 44 | 44 | 44 |
| A | B | C | D | |
| 10 | ||||
| 1 | 2 | 3 | 4 | 10 |
| 5 | 2 | -1 | 4 | 10 |
| 0 | 3 | 6 | 1 | 10 |
| 4 | 3 | 2 | 1 | 10 |
| 10 | 10 | 10 | 10 | 10 |
| A | B | C | D | |
| 48 | ||||
| 12 | 12 | 12 | 12 | 48 |
| 13 | 11 | 9 | 15 | 48 |
| 10 | 14 | 14 | 10 | 48 |
| 13 | 11 | 13 | 11 | 48 |
| 48 | 48 | 48 | 48 | 48 |
| A | B | C | D | |
| 24 | ||||
| 6 | 6 | 6 | 6 | 24 |
| 7 | 5 | 3 | 9 | 24 |
| 4 | 8 | 8 | 4 | 24 |
| 7 | 5 | 7 | 5 | 24 |
| 24 | 24 | 24 | 24 | 24 |
Autor: Ricardo Silva - outubro/2025
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
[1] https:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato