Página de estudos de matemática e sequências numéricas

Números Triangulares Quadrados Perfeitos - 443

Números triangulares quadrados perfeitos são números que ao mesmo tempo são triangulares e quadrados.

Números triangulares, também denominados de números figurados, números geométricos, números poligonais, são números que podem formar figuras geométricas de triângulos por meio de arranjos de pontos.

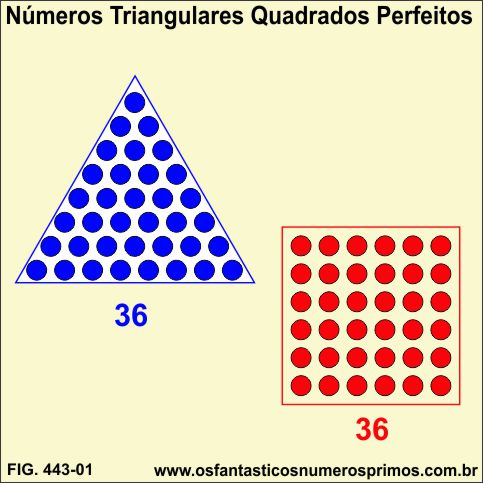
Número quadrado perfeito é um número que multiplicado por ele mesmo tem como resultado um outro número inteiro e a sua raiz quadrada é também um número inteiro.

Números quadrados perfeitos também podem ser formados por meio de arranjos de pontos formando figuras geométricas de quadrados.

O estudo demonstra como se gerar números triangulares quadrados perfeitos a partir da própria sequência de números triangulares quadrados perfeitos.

Ordens / posições de termos em sequências numéricas

Determinadas sequências numéricas têm as ordens / posições de seus termos naturalmente na própria sequência numérica.

Números Naturais

Na sequência de números naturais, os próprios termos são suas ordens / posições e assim sucessivamente...

Não há a necessidade de fazer cálculos para se saber a ordem / posição de um número natural.

Números Quadrados Perfeitos

Multiplicando-se número natural por ele mesmo, obtem-se um quadrado perfeito e próprio número natural é a ordem / posição de um número quadrado perfeito.

O mesmo acontece com as sequências de números cúbicos, números de quarta potência, etc.

Números triangulares

Para se saber qual é o número triangular de ordem / posição 11, devemos efetuar cálculos aritméticos ou algébricos, por exemplo: o produto de dois números consecutivos dividido por 2 tem como resultado um número triangular.

(11 x 12) / 2 = 66

66 é um número triangular de ordem / posição 11, isto é, de décima primeira posição.

Primeiros 12 Números triangulares Quadrados

A tabela a seguir apresenta os 12 primeiros números triangulares quadrados.

Diferença entre raízes quadradas

Na coluna diferença entre raízes é apresentado a subtração entre uma raiz quadrada sucessora e uma raiz quadrada antecessora de um número triangular quadrado perfeito.

As diferenças, aparentemente, são números expressivos e dispersos, não apresentando nenhuma regularidade, mas...

...efetuando-se diferenças das diferenças, as diferenças das diferenças são múltiplos das raízes quadradas correspondentes.

As diferenças das diferenças são 4 vezes as raízes quadradas correspondentes:

24 : 6 = 4

140 : 35 = 4

816 : 204 = 4

4.756 : 1.189 = 4

Diferença entre raízes quadradas e ternos pitagóricos

A diferença entre raízes quadradas de números triangulares quadrados perfeitos geram os terceiros termos, isto é, as hipotenusas de Ternos Pitagóricos Raros.

Ternos Pitagóricos Raros são ternos cuja diferença entre os catetos é de 1 unidade.

Diferença entre raízes quadradas e Escada de Theon

A diferença entre raízes quadradas de números triangulares quadrados perfeitos correspondem aos mesmos termos da sequência (a) de ordens / posições ímpares da Escada de Theon.

Diferença entre números triangulares quadrados

Na coluna diferença entre número triangular quadrado é apresentado a subtração de um número triangular quadrado sucessor com um antecessor.

A diferença entre um número triangular quadrado tem como resultado a raiz quadrada de outro número triangular quadrado de ordem / posição ímpar (células coloridas).

A partir destas regularidades numéricas, números triangulares quadrados podem gerados de outros dois números triagulares quadrados.

Multiplicações em diagonais na Escada de Theon

A múltiplicação em diagonal de um termo antecedente da sequência (a) por um termo subsequente da sequência (b) e vice-versa da Escada de Theon têm como resultados números consecutivos.

Exemplos:

2 e 3

15 e 14

84 e 85

A soma dos produtos

A soma dos produtos têm como resultados termos da Sequência (a) da Escada de Theon.

O produto dos produtos

Os produtos dos produtos têm como resultados números triangulares retangulares.

Gerando números triangulares quadrados

Observação importante: os números entre colchetes se referem às ordens / posições das respectivas raízes quadradas de seus números triangulares quadrados.

a)1.189 é raiz quadrada de 1.413.721

[3] 1.225 - [2] 36 = [5] 1.189

1.189 é fator do quinto triangular quadrado / raiz quadrada

Somando as posisões [2] + [3] = [5]

b) 40.391 é raiz quadrada de 1.631.432.881

[4] 41.616 - [3] 1.225 = [7] 40.391

40.391 é fator do sétimo triangular / raiz quadrada

somando as posições 4 + 3 = 7

c) 1.372.105 é raiz quadrada de 1.882.672.131.025

[5] 1.413.721 - [4] 41.616 = [9] 1.372.105

1.372.105 é fator do nono triangular quadrado / raiz quadrada

somando posições 5 + 4 = 9

d) 46.611.179 é raiz quadrada de 2.172.602.007.770.041

[6] 48.024.900 - [5] 1.413.721 = [11] 46.611.179

46.611.179 é fator do décimo primeiro triangular quadrado / raiz quadrada

somando as posições 6 + 5 = 11

e) 1.583.407.981 é raiz quadrada de 2.507.180.834.294.496.361

[7] 1.631.432.881 - [6] 48.024.900 = [13] 1.583.407.981

1.583.407.981 é fator do décimo terceiro triangular quadrado / raiz quadrada

somando posições 7 + 6 = 13

f) 53.789.260.175 raiz quadrada de 2.893.284.510.173.841.030.625

[8] 55.420.693.056 - [7] 1.631.432.881 = [15] 53.789.260.175

53.789.260.175 é fator do décimo quinto triangular quadrado / raiz quadrada

somando as posições 8 + 7 = 15

Números triangulares quadrados e números consecutivos

1º Triangular quadrado

1 x 1 = 1

1 X 2 consecutivos = rentangular 2

O fator 1 é um quadrado perfeito

2º Triangular quadrado

6^² = 36

8 x 9 consecutivos = rentangular 72

O fator 9 é um quadrado perfeito

3º Triangular quadrado

35^² = 1.225

49 x 50 consecutivos = retangular 2.450

O fator 49 é um quadrado perfeito

4º Triangular quadrado

204^² = 41.616

288 x 289 consecutivos =retangular 83.232

O fator 289 é um quadrado perfeito

5º Triangular quadrado

1.189^² = 1.413.721

1681 x 1682 consecutivos = retangular 2.827.442

O fator 1681 é um quadrado perfeito

6º Triangular quadrado

6.930^² = 48.024.900

9.800 x 9.801 consecutivos = retangular 96.049.800

O fator 9801 é um quadrado perfeito

7º Triangular quadrado

40.391^² = 1.631.432.881

57.121 x 57.122 consecutivos = retangular 3.262.865.762

O fator 57.121 é um quadrado perfeito

8º Triangular quadrado

235.416^² = 55.420.693.056,

332.928 x 332.929 consecutivos = retangular 110.841.386.112

O fator 332.929 é um quadrado perfeito

9º Triangular quadrado

1372105^² = 1.882.672.131.025,

1.940.449 x 1940450 consecutivos = retangular 3765344262050

O fator 1.940.449 é um quadrado perfeito

10º Triangular quadrado

7997214^² = 63.955.431.761.796,

11309768 x 11309769 consecutivos = retangular 127910863523592

O fator 11.309.769 é um quadrado perfeito

11º Triangular quadrado

46611179^² = 2.172.602.007.770.041

65918161 x 65918162 consecutivos = retangular 4.345.204.015.540.082

O fator 65.918.161 é um quadrado perfeito

12º Triangular quadrado

271.669.860^² = 73.804.512.832.419.600.

384.199.200 x 384.199.201 consecutivos = retangular 147.609.025.664.839.200

O fator 384.199.201 é um quadrado perfeito

13º Triangular quadrado

1.583.407.981^² = 2.507.180.834.294.496.361

raiz do dobro do quadrado:

√5.014.361.668.588.992.722

= 2239277041,4999999999441784121913

2.239.277.041 x 2.239.277.042 (consecutivos) = 5.014.361.668.588.992.722

5.014.361.668.588.992.722 : 2 = 2.507.180834.294.496.361

O fator 2.239.277.041 é um quadrado perfeito

15º Triangular quadrado

53.789.260.175^² = 2.893.284.510.173.841.030.625

raiz do dobro do quadrado:

√5.786.569.020.347.682.061.250

= 76069501249,499999999998356765879

76.069.501.249 x 76.069.501.250 (consecutivos) = 5.786.569.020.347.682.061.250

5.786.569.020.347.682.061.250 : 2 = 2.893.284.510. 173.841.030.625

O fator 76.069.501.249 é um quadrado perfeito

Fórmula da raíz quadrada de Número Triangular Quadrado

Se a raiz quadrada da metade da multiplicação de 2 números consecutivos, sendo um dos fatores, um quadrado perfeito ímpar, for um número inteiro, então esse número e a raiz quadrada de um número triangular quadrado perfeito.

Exemplo 1)

Exemplo 2)

Autor: Ricardo Silva - junho/2023

Fontes Bibliográficas:

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020

SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022

SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

https://en.wikipedia.org/wiki/Square_triangular_number

https://oeis.org/A001110

https://oeis.org/A001110/list

https://numbergenerator.org/numberlist

Matérias relacionadas:

011-estudos-004-soma-numeros-triangulares

011-estudos-015-numeros-triangulares-suas-posicoes-parte-1

011-estudos-025-numeros-triangulares-numeros-perfeitos

011-estudos-444-numeros-triangulares-quadrados-produto-dois-numeros-consecutivos

011-estudos-446-numeros-triangulares-quadrados-perfeitos-e-o-numero-oito

011-estudos-447-escada-de-theon-e-numeros-triangulares-quadrados-perfeitos

011-estudos-466-numeros-triangulares-retangulares

Livro digital (e-book)

Números Primos e o

Método Números Atraentes

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Progressões Aritméticas e Geométricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Tabuada de Pythagoras

e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Estudos de Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Os Fantásticos Números Primos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Ternos Pitagóricos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

Recebam GRATUITAMENTE

o E-book

Triângulo Retângulo

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Livro Digital (e-book) Descobrindo Números Primos a partir de Números Compostos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (E-book) Quadrados Mágicos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Triangulares e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual digital (E-book) Quadrado Mágico Triplo

LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Números Perfeitos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Multiplicação através da soma de múltiplos

LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.