


Números Triangulares, também denominados de números figurados, são números que podem ser formados por meio de arranjos de pontos formando figuras geométricas de triângulos.
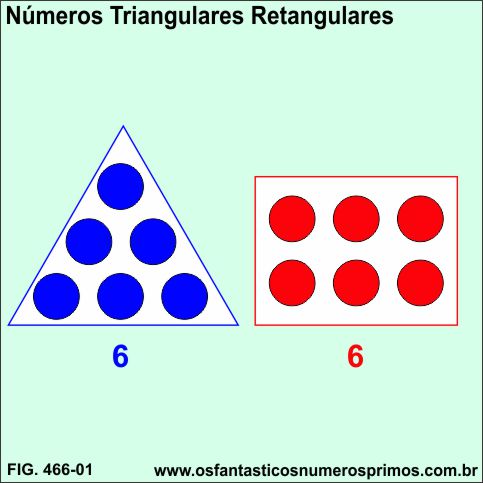
Podemos obter números triangulares através:
a) soma de números naturais consecutivos;
1
1 + 2 = 3
1 + 2 + 3 = 6
b) do produto de 2 números consecutivos dividido por 2;
(1 x 2) / 2 = 1
(2 x 3) / 2 = 3
(3 x 4) / 2 = 6
Números retangulares também são números figurados e podem ser formados por meio de arranjos de pontos formando figuras geométricas de retângulos.
Podemos obter números retangulares através:
a) da soma de números pares consecutivos;
2
2 + 4 = 6
2 + 4 + 6 = 12
b) do produto de 2 números naturais consecutivos
1 x 2 = 2
2 x 3 = 6
3 x 4 = 12
Números Triangulares Retangulares são números que ao mesmo tempo são números triangulares e retangulares.
A tabela a seguir demonstra os 20 primeiros produtos de 2 números consecutivos divididor por 2 e entre eles:
a) o número retangular 6 que pode ser gerado do produto de 2 x 3, como também do produto de 3 x 4 dividido por 2;
b) o número retangular 210 que poder ser gerado do produto de 14 x 15, bem como do produto de 20 x 21 dividido por 2.
6 e 210 são exemplos de números triangulares retangulares.
| Números Triangulares Retangulares | ||||
| números | ||||
| consecutivos | divisão | |||
| (produto) | por 2 | |||
| ordem / | naturais | naturais | retangular | triangular |
| posição | ||||
| 1 | 1 | 2 | 2 | 1 |
| 2 | 2 | 3 | 6 | 3 |
| 3 | 3 | 4 | 12 | 6 |
| 4 | 4 | 5 | 20 | 10 |
| 5 | 5 | 6 | 30 | 15 |
| 6 | 6 | 7 | 42 | 21 |
| 7 | 7 | 8 | 56 | 28 |
| 8 | 8 | 9 | 72 | 36 |
| 9 | 9 | 10 | 90 | 45 |
| 10 | 10 | 11 | 110 | 55 |
| 11 | 11 | 12 | 132 | 66 |
| 12 | 12 | 13 | 156 | 78 |
| 13 | 13 | 14 | 182 | 91 |
| 14 | 14 | 15 | 210 | 105 |
| 15 | 15 | 16 | 240 | 120 |
| 16 | 16 | 17 | 272 | 136 |
| 17 | 17 | 18 | 306 | 153 |
| 18 | 18 | 19 | 342 | 171 |
| 19 | 19 | 20 | 380 | 190 |
| 20 | 20 | 21 | 420 | 210 |
| www.osfantasticosnumerosprimos.com.br | ||||
O presente estudo demonstra que a partir do Algoritmo Escada de Theon em que multiplicando os termos das sequências (a) e (b) em diagonais são gerados duas sequências numéricas de números consecutivos que geram números triangulares retangulares.
Theon de Smyrna (70 d. C. e 135 d. C) foi um filósofo e matemático grego, autor da obra “Matemáticas para entender Platão“ uma compilação introdutória da matemática grega. A obra do platônico inglês Thomas Taylor (1758-1835) “The Theoretic Arithmetic of the Pytagoreans“ divulgou amplamente o conhecimento deste livro na cultura ocidental. Um segundo trabalho sobre a ordem de estudo das obras de Platão foi descoberto em uma tradução árabe.[1][2].
Theon de Smyrna também é autor de um dispositivo numérico, isto é, um algoritmo que leva o seu nome Escada de Theon com o qual é possível de se extrair a raiz quadrada de 2 (√2), como também ser adaptado para se extrair a raiz de qualquer número natural.
Dividindo-se os termos correspondentes b / a, o quociente tende a raiz quadrada de 2:
√2 = 1,4142
| Algoritmo Escada de Theon | ||
| sequência | sequência | razão |
| a | b | b / a |
| 1 | 1 | 1/1 = 1 |
| 2 | 3 | 3 / 2 = 1,5 |
| 5 | 7 | 7 / 5 =1,4 |
| 12 | 17 | 17 / 12 = 1,41666... |
| 29 | 41 | 41 / 29 = 1,41379... |
| 70 | 99 | 99 / 70 = 1,41428... |
| 169 | 239 | 239 / 169 = 1,41420... |
Fonte: adaptado de Tópicos de História da Matemática[3]
O Algoritmo Escada de Theon apresenta outra propriedade interessante, a partir dos produtos de 2 termos correspondentes, podem ser gerados raízes quadradas de Números Triangulares Quadrados Perfeitos.
Interessante observar que os números crescem rapidamente.
Para mais informações, veja matérias relacionadas abaixo!
| Escada de Theon | ||||
| e | ||||
| Números Triangulares Quadrados Perfeitos | ||||
| ordem / | a | b | produto | Triangular |
| posição | (raiz quadrada) | Quadrado Perfeito | ||
| 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 3 | 6 | 36 |
| 3 | 5 | 7 | 35 | 1225 |
| 4 | 12 | 17 | 204 | 41616 |
| 5 | 29 | 41 | 1189 | 1413721 |
| 6 | 70 | 99 | 6930 | 48024900 |
| 7 | 169 | 239 | 40391 | 1631432881 |
| 8 | 408 | 577 | 235416 | 55420693056 |
| 9 | 985 | 1393 | 1372105 | 1882672131025 |
| 10 | 2378 | 3363 | 7997214 | 63955431761796 |
| www.osfantasticosnumerosprimos.com.br | ||||
Multiplicando um termo da sequência (a) por um termo da sequência (b) em diagonal, de cima para baixo.
Exemplos:
1 x 3 = 3 (o 3 está na coluna d)
2 x 7 = 14 ( o 14 está na coluna d)
Multiplicando um termo da sequência (b) por um termo da sequência (b) em diagonal, de baixo para cima.
Exemplos:
1 x 2 = 2 (o 3 está na coluna c)
3 x 5 = 15 ( o 15 está na coluna c)
Desta forma obtêm-se duas novas sequências numéricas nas colunas (c) e (d) cujos termos correspondentes são números consecutivos alternados.
| Escada de Theon | ||||
| e multiplicação em diagonal | ||||
| ordem / | a | b | c | d |
| posição | ||||
| 1 | 1 | 1 | 2 | 3 |
| 2 | 2 | 3 | 15 | 14 |
| 3 | 5 | 7 | 84 | 85 |
| 4 | 12 | 17 | 493 | 492 |
| 5 | 29 | 41 | 2870 | 2871 |
| 6 | 70 | 99 | 16731 | 16730 |
| 7 | 169 | 239 | 97512 | 97513 |
| 8 | 408 | 577 | 568345 | 568344 |
| 9 | 985 | 1393 | 3312554 | 3312555 |
| 10 | 2378 | 3363 | 19306983 | 19306982 |
| www.osfantasticosnumerosprimos.com.br | ||||
Os produtos de números consecutivos das colunas (c) e (d) gerados dos termos do Algoritmo Escada de Theon têm como resultados números triangulares retangulares.
| Escada de Theon e | |||
| Números Triangulares Retangulares | |||
| ordem / | c | d | Números Triangulares |
| posição | Retangulares | ||
| 1 | 2 | 3 | 6 |
| 2 | 15 | 14 | 210 |
| 3 | 84 | 85 | 7140 |
| 4 | 493 | 492 | 242556 |
| 5 | 2870 | 2871 | 8239770 |
| 6 | 16731 | 16730 | 279909630 |
| 7 | 97512 | 97513 | 9508687656 |
| 8 | 568345 | 568344 | 323015470680 |
| 9 | 3312554 | 3312555 | 10973017315470 |
| 10 | 19306983 | 19306982 | 372759573255306 |
| www.osfantasticosnumerosprimos.com.br | |||
Outra propriedade relacionada a Escada de Theon é que decompondo cada termo das sequências (a) e (b) de ordens / posições ímpares, começando da ordem / posição 3 como números consecutivos e posteriormente multiplicando-os, obtêm-se também números triangulares retangulares.
Exemplos:
5 pode ser decomposto nos números consecutivos 2 e 3.
O produto de 2 com 3 é o triangular 6.
2 x 3 = 6
7 pode ser decomposto nos números consecutivos 3 e 4.
O produto de 3 com 4 dividido por 2 é igual ao triangular 6
(3 x 4) / 2 = 6
Nestas demonstrações ficam patentes que determinados números triangulares retangulares possuem a propriedade de serem gerados por 2 duplas de números consecutivos distintos extraídos do Algortimo Escada de Theon cujos termos são de ternos pitagóricos raros.
3 - 4 - 5
20 - 21 - 29
119 - 120 - 169
e outros.
Lembrando que somente números ímpares podem ser a soma de 2 números consecutivos.
| Algortimo Escada de Theon e | ||||||||
| Números Triangulares Retangulares | ||||||||
| ordem / | sequência (a) | números | produto | sequência (b) | números | produto | ||
| posição | consecutivos | (triangular | consecutivos | (triangular | ||||
| retangular) | retangular) | |||||||
| 1 | 1 | 1 | ||||||
| 2 | 2 | 3 | ||||||
| 3 | 5 | ( 2 x 3 ) | = | 6 | 7 | ( 3 x 4 ) / 2 | = | 6 |
| 4 | 12 | 17 | ||||||
| 5 | 29 | ( 14 x 15 ) | = | 210 | 41 | ( 20 x 21 ) / 2 | = | 210 |
| 6 | 70 | 99 | ||||||
| 7 | 169 | ( 84 x 85 ) | = | 7140 | 239 | ( 119 x 120 ) / 2 | = | 7140 |
| 8 | 408 | 577 | ||||||
| 9 | 985 | ( 492 x 493 ) | = | 242556 | 1393 | ( 696 x 697 ) / 2 | = | 242556 |
| 10 | 2378 | 3363 | ||||||
| 11 | 5741 | ( 2870 x 2871 ) | = | 8239770 | 8119 | ( 4059 x 4060 ) / 2 | = | 8239770 |
| 12 | 13860 | 19601 | ||||||
| 13 | 33461 | ( 16730 x 1671 ) | = | 279909630 | 47321 | ( 23660 x 23661 ) / 2 | = | 27990630 |
| 14 | 80782 | 114243 | ||||||
| 15 | 195025 | ( 97512 x 97513 ) | = | 9508687656 | 275807 | ( 137903 x 137904 ) / 2 | = | 9508687656 |
| www.osfantasticosnumerosprimos.com.br | ||||||||
No estudo:
011-estudos-399-somas-pares-divisores-numero-natural
são demonstrados que determinados números naturais têm as somas de pares de divisores números primos e entre eles aparacem os números 6 e 210 que são números triangulares retangulares.
Um outro fato a observar é que os pares de divisores correspondentes de 6 e 210 são formados por números ímpares e pares e vice-versa, isto é, ora, é um ímpar com par, ora é um par com ímpar. Nos pares de divisores não aparecem ímpar com ímpar e nem par com par juntos.
D(6)={1, 2, 3, 6}
4 divisores
Todas as somas têm resultados números ímpares primos.
| Soma de pares de divisores de 210 | |||||||
| quant. | divisor | divisor | soma | ||||
| pares | |||||||
| 1 | 1 | + | 6 | = | 7 | primo | |
| 2 | 2 | + | 3 | = | 5 | primo | |
| www.osfantasticosnumerosprimos.com.br | |||||||
D(210)={1, 2, 3, 5, 6 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210}
16 divisores
Todas as somas têm resultados números ímpares primos.
| Soma de pares de divisores de 210 | |||||||
| quant. | divisor | divisor | soma | ||||
| pares | |||||||
| 1 | 1 | + | 210 | = | 211 | primo | |
| 2 | 2 | + | 105 | = | 107 | primo | |
| 3 | 3 | + | 70 | = | 73 | primo | |
| 4 | 5 | + | 42 | = | 47 | primo | |
| 5 | 6 | + | 35 | = | 41 | primo | |
| 6 | 7 | + | 30 | = | 37 | primo | |
| 7 | 10 | + | 21 | = | 31 | primo | |
| 8 | 14 | + | 15 | = | 29 | primo | |
| www.osfantasticosnumerosprimos.com.br | |||||||
O número triangular retangular 7140 possui 48 divisores.
Na formação de pares de divisores, diferentemente dos números 6 e 210, há grupos de divisores formados somente por número pares.
As somas têm resultados números ímpares e pares.
| Soma de pares de divisores de 7140 | |||||||
| quant. | divisor | divisor | soma | ||||
| pares | |||||||
| 1 | 1 | + | 7140 | = | 7141 | ||
| 2 | 2 | par | + | par | 3570 | = | 3572 |
| 3 | 3 | + | 2380 | = | 2383 | ||
| 4 | 4 | + | 1785 | = | 1789 | ||
| 5 | 5 | + | 1428 | = | 1433 | ||
| 6 | 6 | par | + | par | 1190 | = | 1196 |
| 7 | 7 | + | 1020 | = | 1027 | ||
| 8 | 10 | par | + | par | 714 | = | 724 |
| 9 | 12 | + | 595 | = | 607 | ||
| 10 | 14 | par | + | par | 510 | = | 524 |
| 11 | 15 | + | 476 | = | 491 | ||
| 12 | 17 | + | 420 | = | 437 | ||
| 13 | 20 | + | 357 | = | 377 | ||
| 14 | 21 | + | 340 | = | 361 | ||
| 15 | 28 | + | 255 | = | 283 | ||
| 16 | 30 | par | + | par | 238 | = | 268 |
| 17 | 34 | par | + | par | 210 | = | 244 |
| 18 | 35 | + | 204 | = | 239 | ||
| 19 | 42 | par | + | par | 170 | = | 212 |
| 20 | 51 | + | 140 | = | 191 | ||
| 21 | 60 | + | 119 | = | 179 | ||
| 22 | 68 | + | 105 | = | 173 | ||
| 23 | 70 | par | + | par | 102 | = | 172 |
| 24 | 84 | + | 85 | = | 169 | ||
| www.osfantasticosnumerosprimos.com.br | |||||||
Autor: Ricardo Silva - setembro/2023
[3] PITOMBEIRA, João Bosco, ROQUE, Tatiana. Tópicos de História da Matemática. Edição Digital
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
[1]https://es.wikipedia.org/wiki/
[2]https://www.matematicaparafilosofos.pt/

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato