


Ternos Pitagóricos são grupos de 3 números inteiros que tem relação com o Teorema de Pitágoras cujo enunciado é: "O quadrado da hipotenusa é igual a soma dos quadrados dos catetos" ou " A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa" e que são representados pelas seguintes fórmulas:
| a² = b² + c² |
ou
| a² + b² = c² |
Terno pitagórico primitivo é o terno cujos termos são primos entre si, isto é, o mdc (a,b,c)=1 e terno pitagórico derivado é o terno cujos termos não são primos entre si, isto é, o mdc (a,b,c)>1.

Conforme estudos publicados no livro digital (e-book) Ternos Pitagóricos e Sequências Numéricas, bem como, aqui no WebSite Os Fantásticos Números Primos, ternos pitagóricos são classificados segundo padrões e regularidades numéricas ao serem gerados pelas Fórmulas de Euclides:
a) Ternos Pitagóricos Primitivos de Ordem Triangular;
b) Ternos Pitagóricos Primitivos de Ordem Não Triangular;
c) Ternos Pitagóricos Derivados Pares;
d) Ternos Pitagóricos Derivados Ímpares;
e) Ternos Pitagóricos Raros;
Conheça também terno pitagórico triangular, em Matérias Relacionadas, abaixo!
O presente estudo demonstram 3 fórmulas desenvolvidas pelo Professor Fernando Manso (Universidade Tecnológica Federal do Paraná - UTFPR-CM) com as quais são possíveis de se gerarem ternos pitagóricos primitivos a partir da medida da hipotenusa.
Observação importante:
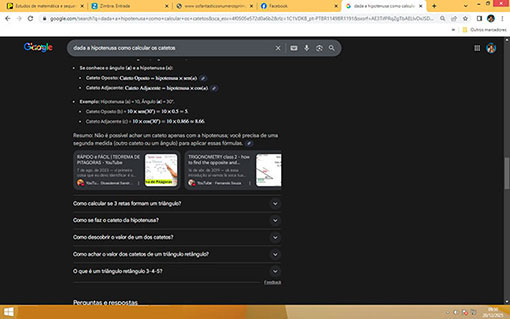
Antes de receber e conhecer as fórmulas do Professor Fernando Manso, fez-se a seguinte pesquisa ao Navegador Google, na data de 20/12/2025: Dada a hipotenusa, como calcular os catetos ?
Entre vários resultados, aparece a seguinte resposta:
"Resumo: Não é possível achar um cateto apenas com a hipotenusa; você precisa de uma segunda medida (outro cateto ou ângulo) para aplicar essas fórmulas."
Números de Fermat da Forma 4x + 1 são números múltiplos de 4 somados 1 unidade.
Entre os números da Forma 4x + 1, há:
a) números primos que podem ser escritos como soma de 2 quadrados de um único modo, isto é, uma única dupla como soma de 2 quadrados;
b) números compostos que podem ser escritos com soma de 2 quadrados de mais de um modo, isto é, mais de 1 dupla como soma de 2 quadrados;
c) números que não podem ser escritos como soma de 2 quadrados, exemplos: 21, 33, 57 e outros.
Números de Fermat da Forma 4x + 3 não podem ser escritos como soma de 2 quadrados.
Nos números da forma 4x + 1, a variável x (xis) pode ser:
4x ( triangular ) + 1
4x ( retangular ) + 1
4x ( quadrado perfeito ) + 1
4x ( 4x + 3 ) + 1
Números da forma 4x + 3 deixam resto 3 na divisão por 4.
Fórmula Professor Fernando Manso - 1:
| ( 4Tn + 1 )2 = (4Tn)2 + (2n+1)2 |
onde Tn é o n-ésimo número triangular.
Exemplo 1)
i) n = 2
ii) Tn = 3
iii) (4 x 3 + 1 )2 = ( 4 x 3 )2 + ( 2 x 2 + 1)2;
iv) 132 = 122 + 52;
Exemplo 2)
i) n = 6
ii) Tn = 21
iii) (4 x 21 + 1 )2 = ( 4 x 21 )2 + ( 2 x 6 + 1)2;
iv) 852 = 842 + 132;
Interessante destacar que:
a) a Fórmula PFM - 1 geram ternos cujas ordens / posições são de números triangulares (as mesmas das Fórmulas de Euclides);
b) os catetos menor é a sequência de números ímpares a partir de 3.
| Ternos Pitagóricos Primitivos de Ordem Triangular | ||||
| Fórmula PFM - 1 | ||||
| hipotenusa | cateto | cateto | ||
| maior | menor | |||
| ordem / | ||||
| posição | triangular | [ 4(Tn) + 1 ]2 | [ 4(Tn) ]2 | ( 2n+1 )2 |
| 1 | 1 | 5 | 4 | 3 |
| 2 | 3 | 13 | 12 | 5 |
| 3 | 6 | 25 | 24 | 7 |
| 4 | 10 | 41 | 40 | 9 |
| 5 | 15 | 61 | 60 | 11 |
| 6 | 21 | 85 | 84 | 13 |
| 7 | 28 | 113 | 112 | 15 |
| 8 | 36 | 145 | 144 | 17 |
| 9 | 45 | 181 | 180 | 19 |
| 10 | 55 | 221 | 220 | 21 |
| www.osfantasticosnumerosprimos.com.br | ||||
Fórmula Professor Fernando Manso - 2:
| ( 4n^2 + 1 )2 = ( 4n^2 - 1 )2 + ( 4n )2 |
onde n é número natural (número quadrado e sua raiz)
Exemplo
i) n = 13
ii) ( 4n2 + 1 )2 = ( 4n2 - 1 )2 + ( 4n )2
iii) ( 4.132 + 1 )2 = ( 4.132 - 1 )2 + ( 4.13 )2
iv) 6772 = 6752 + 522
Interessante destacar que:
a) a Fórmula PFM - 2 geram ternos cujas ordens / posições não são de números triangulares;
b) as hipotenusas são 1 unidade maior que um quadrado perfeito (entre eles, Números de Fermat (2^2^n)+1 );
c) os catetos maior são 1 unidade menor que um número quadrado perfeito, exceto o primeiro terno 3-4-5 (entre eles, Numeros de Mersenne 2^n - 1 );
d) a soma da hipotenusa com o cateto maior tem como resultado a metade do quadrado perfeito do cateto menor.
| Ternos Pitagóricos Primitivos de Ordem Não Triangular | |||
| Fórmula PFM - 2 | |||
| n | hipotenusa | cateto | cateto |
| maior | menor | ||
| [4n2 + 1]2 | [4n2 - 1]2 | (4n)2 | |
| 1 | 5 | 3 | 4 |
| 2 | 17 | 15 | 8 |
| 3 | 37 | 35 | 12 |
| 4 | 65 | 63 | 16 |
| 5 | 101 | 99 | 20 |
| 6 | 145 | 143 | 24 |
| 7 | 197 | 195 | 28 |
| 8 | 257 | 255 | 32 |
| 9 | 325 | 323 | 36 |
| 10 | 401 | 399 | 40 |
| www.osfantasticosnumerosprimos.com.br | |||
Fórmula Professor Fernando Manso - 3:
| n2 = ( n-k2 )2 + [ k ( 2n-k2 )1/2 ]2 |
se n for um número que subtraído 1 unidade e dividido por 4 não tiver como quociente um número triangular e nem um número quadrado perfeito.
Exemplo com o número 29.
etapa 1)
(29 - 1) / 4 = 7
etapa 2)
7 não é um número triangular e nem quadrado perfeito
etapa 3)
encontrar um inteiro ímpar k>1 tal que 2n-k2 seja um quadrado perfeito;
etapa 4)
não podemos precisar o valor de k, ele precisa ser encontrado testanto os valores ímpares a partir do 3.
etapa 5)
para k = 3;
2 x 29 - 32 = 58 - 9 = 49 que é um quadrado perfeito.
Assim, a fórmula 3 nos dá o terno pitagórico:
292 = ( 29 - 32 )2 + [ 3 ( 58 - 32 )1/2 ]2;
292 = 202 + 212.
A presente tabela demonstram alguns números primos da forma 4x + 1 com a utilização da Fórmula PFM - 3.
| Ternos Pitagóricos Primitivos | |||||||||
| Fórmula PFM - 3 | |||||||||
| 4x+1 | quadrado | quadrado | soma | ||||||
| (número | cateto | cateto | quadrado | cateto | cateto | quadrados | |||
| primo) | dobro | hipotenusa | ......menor..... | .......maior.......... | hipotenusa | menor | .........maior.......... | catetos | |
| k | n | n | n | ( n-k2 ) | [ k ( 2n-k2 )1/2 ] | n2 | ( n-k2 )2 | [ k ( 2n-k2 )1/2 ]2 | |
| 3 | 29 | 58 | 29 | 20 | 21 | 841 | 400 | 441 | 841 |
| 5 | 53 | 106 | 53 | 28 | 45 | 2809 | 784 | 2025 | 2809 |
| 5 | 73 | 146 | 73 | 48 | 55 | 5329 | 2304 | 3025 | 5329 |
| 3 | 89 | 178 | 89 | 80 | 39 | 7921 | 6400 | 1521 | 7921 |
| 5 | 97 | 194 | 97 | 72 | 65 | 9409 | 5184 | 4225 | 9409 |
| 7 | 109 | 218 | 109 | 60 | 91 | 11881 | 3600 | 8281 | 11881 |
| 7 | 137 | 274 | 137 | 88 | 105 | 18769 | 7744 | 11025 | 18769 |
| 3 | 149 | 298 | 149 | 140 | 51 | 22201 | 19600 | 2601 | 22201 |
| 5 | 157 | 314 | 157 | 132 | 85 | 24649 | 17424 | 7225 | 24649 |
| 11 | 173 | 346 | 173 | 52 | 165 | 29929 | 2704 | 27225 | 29929 |
| 5 | 193 | 386 | 193 | 168 | 95 | 37249 | 28224 | 9025 | 37249 |
| www.osfantasticosnumerosprimos.com.br | |||||||||
Determinados números da forma 4x + 1 ao serem subtraídos 1 unidade e divididos por 4, apresentam quocientes que não são nem números triangulares e nem números quadrados perfeitos, como se constata, são quocientes que não há uniformidade, são números díspares.
| (número | menos | diferença | divisão por 4 |
| primo) | 1 | quociente | |
| 4x + 1 | unidade | ||
| 29 | 1 | 28 | 7 |
| 53 | 1 | 52 | 13 |
| 73 | 1 | 72 | 18 |
| 89 | 1 | 88 | 22 |
| 97 | 1 | 96 | 24 |
| 109 | 1 | 108 | 27 |
| 137 | 1 | 136 | 34 |
| 149 | 1 | 148 | 37 |
| 157 | 1 | 156 | 39 |
| 173 | 1 | 172 | 43 |
| 193 | 1 | 192 | 48 |
| www.osfantasticosnumerosprimos.com.br | |||
Outro método de se constatar a não uniformidade de determinados números da forma 4x + 1 é decompô-los como soma de 2 números consecutivos.
Para mais informações, veja abaixo, Matérias Relacionadas!
Exemplos:
a) número 29
14 + 15 = 29
tanto a parcela 14 e 15 não são números retangulares.
b) número 53
26 + 27 = 53
tanto a parcela 26 e 27 não são números retangulares.
c) número 73
36 + 37 = 73
tanto a parcela 36 e 37 não são números retangulares.
Autor: Ricardo Silva - janeiro/2026
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato