


Terno pitagórico é um grupo de três números inteiros que satisfazem ao Teorema de Pitágoras: A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa (a² + b² = c²), isto é, dois números que elevados ao quadrado e depois somados (a² + b²) tem como resultado um número quadrado perfeito (c²) e que depois de extraído a sua raiz quadrada, o resultado é também um número inteiro.
Euclides, em seu livro Elementos, demonstrou que existe uma infinidade de ternos pitagóricos primitivos. Além disso, encontrou fórmulas que geram todos os ternos pitagóricos primitivos. Dados dois números naturais m>n, o terno (a,b,c), onde:
a = m² - n²
b = 2mn
c = m² + n²
é pitagórico, e é primitivo se e somente se m e n são primos entre si e possuem paridades distintas.
Fonte: https://pt.wikipedia.org/
Observando as Fórmulas de Euclides, contata-se que uma das equações é justamente a Soma de 2 Quadrados:
| c = m² + n² |
Pierre de Fermat, jurista e entusiasta matemático francês, (1601-1665), entre várias contribuições à Matemática, em carta a Marin Mersenne (1588-1648), datada de 25 de dezembro de 1640, afirma que números da forma 4x + 1 podem ser escritos como a soma de 2 quadrados enquanto números da forma 4x + 3 não podem ser escritos como a soma de 2 quadrados.
O presente estudo demonstram que duplas de números formadas por parcelas cuja soma é um número quadrado perfeito ao serem elevados aos quadrados e somadas geram números da forma 4x + 1 e suas diferenças formam Progressão Aritmética de razão 4 cujos termos são múltiplos de 4.
A partir de subtrações sucessivas e adições sucessivas deduziu o Método Números Atraentes.
Como o Método Números Atraentes são possíveis de saber se determinado número ímpar é um número primo ou não, bem como, saber divisores de um dado número.
Para mais informações, veja abaixo, Matérias Relacionadas!
Efetuando-se subtrações sucessivas cujo minuendo é a constante o número quadrado perfeito 9 e os subtraendos até um número que é quase metade de 9, obtêm-se 4 diferenças.
| Quadrado Perfeito 9 | ||||
| Subtrações Sucessivas | ||||
| minuendo | subtraendo | diferença | ||
| 9 | - | 1 | = | 8 |
| 9 | - | 2 | = | 7 |
| 9 | - | 3 | = | 6 |
| 9 | - | 4 | = | 5 |
| www.osfantasticosnumerosprimos.com.br | ||||
Efetuando-se adições sucessivas com os subtraendos e diferenças que agora são parcelas, obtêm-se 4 duplas de somas cujos resultados são o número quadrado perfeito 9.
| Quadrado Perfeito 9 | ||||
| Adições Sucessivas | ||||
| parcela | parcela | soma | ||
| 1 | + | 8 | = | 9 |
| 2 | + | 7 | = | 9 |
| 3 | + | 6 | = | 9 |
| 4 | + | 5 | = | 9 |
| www.osfantasticosnumerosprimos.com.br | ||||
Elevando-se as parcelas ao quadrado e somando-as, obtêm-se números da forma 4x + 1, isto é, números que são somas de 2 quadrados e, entre eles, números primos.
| Soma de 2 | ||||||||
| Quadrados | ||||||||
| parcela | parcela | quadrado | quadrado | soma | tipo | P.A | ||
| 2 | ||||||||
| quadrados | ||||||||
| 12 | + | 82 | 1 | 64 | 65 | |||
| 22 | + | 72 | 4 | 49 | 53 | primo | 12 | |
| 32 | + | 62 | 9 | 36 | 45 | 8 | ||
| 42 | + | 52 | 16 | 25 | 41 | primo | 4 | |
| www.osfantasticosnumerosprimos.com.br | ||||||||
As diferenças de somas de 2 quadrados cujas raízes são parcelas da soma do quadrado 9 forma uma progressão aritmética - P.A. decrescente de razão -4 e cujos termos são múltiplos de 4.
| soma | diferença | P.A |
| 2 | da soma de | |
| quadrados | 2 quadrados | |
| 65 | ||
| 12 | 12 | |
| 53 | ||
| 8 | 8 | |
| 45 | ||
| 4 | 4 | |
| 41 | ||
| www.osfantasticosnumerosprimos.com.br | ||
Efetuando-se subtrações sucessivas cujo minuendo é a constante o número quadrado perfeito 25 e os subtraendos até um número que é quase metade de 25, obtêm-se 12 diferenças.
| Quadrado Perfeito 25 | ||||
| Subtraçoes Sucessivas | ||||
| minuendo | subtraendo | diferença | ||
| 25 | - | 1 | = | 24 |
| 25 | - | 2 | = | 23 |
| 25 | - | 3 | = | 22 |
| 25 | - | 4 | = | 21 |
| 25 | - | 5 | = | 20 |
| 25 | - | 6 | = | 19 |
| 25 | - | 7 | = | 18 |
| 25 | - | 8 | = | 17 |
| 25 | - | 9 | = | 16 |
| 25 | - | 10 | = | 15 |
| 25 | - | 11 | = | 14 |
| 25 | - | 12 | = | 13 |
| www.osfantasticosnumerosprimos.com.br | ||||
Efetuando-se adições sucessivas com os subtraendos e diferenças que agora são parcelas, obtêm-se 12 duplas de somas cujos resultados são o número quadrado perfeito 25.
| Quadrado Perfeito 25 | ||||
| Adições Sucessivas | ||||
| parcela | parcela | soma | ||
| 1 | + | 24 | = | 25 |
| 2 | + | 23 | = | 25 |
| 3 | + | 22 | = | 25 |
| 4 | + | 21 | = | 25 |
| 5 | + | 20 | = | 25 |
| 6 | + | 19 | = | 25 |
| 7 | + | 18 | = | 25 |
| 8 | + | 17 | = | 25 |
| 9 | + | 16 | = | 25 |
| 10 | + | 15 | = | 25 |
| 11 | + | 14 | = | 25 |
| 12 | + | 13 | = | 25 |
| www.osfantasticosnumerosprimos.com.br | ||||
Elevando-se as parcelas ao quadrado e somando-as, obtêm-se números da forma 4x + 1, isto é, números que são somas de 2 quadrados e, entre eles números primos.
| Soma de | ||||||||
| 2 Quadrados | ||||||||
| subtraendo | diferença | quadrado | quadrado | soma | tipo | |||
| de 2 | ||||||||
| qua- | ||||||||
| drados | ||||||||
| 12 | + | 242 | 1 | 576 | 577 | primo | ||
| 22 | + | 232 | 4 | 529 | 533 | 44 | ||
| 32 | + | 222 | 9 | 484 | 493 | 40 | ||
| 42 | + | 212 | 16 | 441 | 457 | primo | 36 | |
| 52 | + | 202 | 25 | 400 | 425 | 32 | ||
| 62 | + | 192 | 36 | 361 | 397 | primo | 28 | |
| 72 | + | 182 | 49 | 324 | 373 | primo | 24 | |
| 82 | + | 172 | 64 | 289 | 353 | primo | 20 | |
| 92 | + | 162 | 81 | 256 | 337 | primo | 16 | |
| 102 | + | 152 | 100 | 225 | 325 | 12 | ||
| 112 | + | 142 | 121 | 196 | 317 | primo | 8 | |
| 122 | + | 132 | 144 | 169 | 313 | primo | 4 | |
| www.osfantasticosnumerosprimos.com.br | ||||||||
As diferenças de somas de 2 quadrados cujas raízes são parcelas da soma do quadrado 25 forma uma progressão aritmética decrescente de razão -4 cujos termos são múltiplos de 4.
| soma de | diferença | P.A |
| 2 quadrados | da soma de | |
| 2 quadrados | ||
| 577 | ||
| 44 | 44 | |
| 533 | ||
| 40 | 40 | |
| 493 | ||
| 36 | 36 | |
| 457 | ||
| 32 | 32 | |
| 425 | ||
| 28 | 28 | |
| 397 | ||
| 24 | 24 | |
| 373 | ||
| 20 | 20 | |
| 353 | ||
| 16 | 16 | |
| 337 | ||
| 12 | 12 | |
| 325 | ||
| 8 | 8 | |
| 317 | ||
| 4 | 4 | |
| 313 | ||
| www.osfantasticosnumerosprimos.com.br | ||
Efetuando-se subtrações sucessivas cujo minuendo é a constante o número quadrado perfeito 49 e os subtraendos até um número que é quase metade de 49, obtêm-se 24 diferenças.
Os subtraendos e as diferenças elevadas ao quadrado e somadas têm como resultados somas de 2 quadrados que são números da forma 4x + 1.
As diferenças entre as somas de 2 quadrados têm como resultados progressão aritmética - P.A. decrescente de razão -4 cujos termos são múltiplos de 4.
| Quadrado Perfeito 49 | ||||||||||
| Subtraendos e Diferenças | ||||||||||
| e Somas de 2 Quadrados | ||||||||||
| minu- | subtra- | dife- | quadrado | quadrado | soma | tipo | P.A | |||
| endo | endo | rença | de 2 | |||||||
| qua- | ||||||||||
| drados | ||||||||||
| 49 | - | 1 | = | 48 | 1 | 2304 | 2305 | |||
| 49 | - | 2 | = | 47 | 4 | 2209 | 2213 | primo | 92 | |
| 49 | - | 3 | = | 46 | 9 | 2116 | 2125 | 88 | ||
| 49 | - | 4 | = | 45 | 16 | 2025 | 2041 | 84 | ||
| 49 | - | 5 | = | 44 | 25 | 1936 | 1961 | 80 | ||
| 49 | - | 6 | = | 43 | 36 | 1849 | 1885 | 76 | ||
| 49 | - | 7 | = | 42 | 49 | 1764 | 1813 | 72 | ||
| 49 | - | 8 | = | 41 | 64 | 1681 | 1745 | 68 | ||
| 49 | - | 9 | = | 40 | 81 | 1600 | 1681 | 64 | ||
| 49 | - | 10 | = | 39 | 100 | 1521 | 1621 | primo | 60 | |
| 49 | - | 11 | = | 38 | 121 | 1444 | 1565 | 56 | ||
| 49 | - | 12 | = | 37 | 144 | 1369 | 1513 | 52 | ||
| 49 | - | 13 | = | 36 | 169 | 1296 | 1465 | 48 | ||
| 49 | - | 14 | = | 35 | 196 | 1225 | 1421 | 44 | ||
| 49 | - | 15 | = | 34 | 225 | 1156 | 1381 | primo | 40 | |
| 49 | - | 16 | = | 33 | 256 | 1089 | 1345 | 36 | ||
| 49 | - | 17 | = | 32 | 289 | 1024 | 1313 | 32 | ||
| 49 | - | 18 | = | 31 | 324 | 961 | 1285 | 28 | ||
| 49 | - | 19 | = | 30 | 361 | 900 | 1261 | 24 | ||
| 49 | - | 20 | = | 29 | 400 | 841 | 1241 | 20 | ||
| 49 | - | 21 | = | 28 | 441 | 784 | 1225 | 16 | ||
| 49 | - | 22 | = | 27 | 484 | 729 | 1213 | primo | 12 | |
| 49 | - | 23 | = | 26 | 529 | 676 | 1205 | 8 | ||
| 49 | - | 24 | = | 25 | 576 | 625 | 1201 | primo | 4 | |
| www.osfantasticosnumerosprimos.com.br | ||||||||||
A diferença entre números quadrados perfeitos consecutivos têm como resultados a sequência de números ímpares a partir do número 3 e, entre eles, a sequência de números quadrados perfeitos ímpares a partir do quadrado perfeito 9.
Diferentemente, a soma de números quadrados perfeitos consecutivos têm como resultados números ímpares e números pares e, entre eles, quadrados perfeitos que fazem parte do grupo de ternos pitagóricos raros.
Para mais informações, veja abaixo, Matérias Relacionadas!
A soma de 2 quadrados apresentam várias propriedades matemáticas e, entre elas:
a) nas Fórmulas de Euclides que com visto acima, há equação da soma de 2 quadrados;
b) tem como resultados números ímpares e, entre eles, números primos, como também, números quadrados perfeitos;
c) Pierre de Fermat descobriu que todo número da forma 4x + 1 pode ser escrito como soma de 2 quadrados.
Analisando detalhadamente a tabela:
| Quadrado Perfeito 49 |
| Subtraendos e Diferenças |
| e Somas de 2 Quadrados |
contata-se novas relações numéricas envolvendo a soma de 2 quadrados com números triangulares, bem como, com o Algoritmo Escada de Theon.
Observações importantíssimas:
1) o Algoritmo Escada de Theon a priori é utilizado para extração de raiz quadrada;
2) estudos divulgados aqui no WebSite Os Fantásticos Números Primos, bem como, publicados no livro digital Escada de Theon e Sequências Numéricas revelam que com o algoritmo são possíveis de se gerarem sequencialmente ternos pitagóricos raros, bem como, números triangulares quadrados perfeitos.
| Quadrado Perfeito 49 | ||||||||||
| Subtraendos e Diferenças | ||||||||||
| e Somas de 2 Quadrados | ||||||||||
| minu- | subtra- | dife- | quadrado | quadrado | soma | raiz | ||||
| endo | endo | rença | de 2 | |||||||
| qua- | ||||||||||
| drados | ||||||||||
| 49 | - | 9 | = | 40 | 81 | 1600 | 1681 | 41 | ||
| 49 | - | 21 | = | 28 | 441 | 784 | 1225 | 35 | ||
| www.osfantasticosnumerosprimos.com.br | ||||||||||
9 subtraído do quadrado 49 tem como diferença 40.
O quadrado de 9 = 81, somado com o quadrado de 40 = 1600, tem como resultado o quadrado 1681.
A raiz 41 do quadrado 1681 é um termo do Algoritmo Escada de Theon.
21 subtraído do quadrado 49 tem como diferença 28.
O quadrado de 21 = 441, somado com o quadrado de 28 = 784, tem como resultado o quadrado 1225.
A raiz 35 do quadrado 1225 é um termo do Algoritmo Escada de Theon.
Observações importantes:
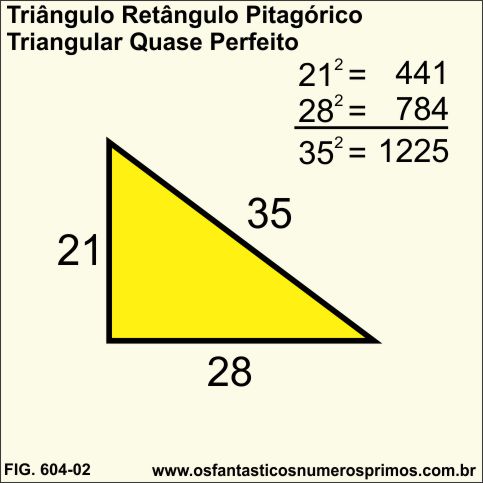
a) os números 21 e 28 são números triangulares consecutivos;
b) a soma de 2 triangulares consecutivos é um número quadrado perfeito;
c) 21 + 28 = 49
d) a figura a seguir apresenta o Primeiro Triângulo Retângulo Pitagórico Triângular Quase Perfeito;
e) os catetos são formados por números triangulares consecutivos, o 21 e 28;
f) a hipotenusa 35 não é número triangular, mas é um termo do Algoritmo Escada de Theon.
Assim como o quadrado 49, encontrou-se os quadrados 289, 441, 529, 961 e 1225 com características quase semelhantes, isto porquê, os subtraendos e as diferenças não são números triangulares.
| quadrado | |||||||||
| minu- | subtra- | diferença | quadra- | quadra- | soma | raiz | |||
| endo | endo | do | do | de | |||||
| 2 | |||||||||
| quadra- | |||||||||
| dos | |||||||||
| 49 | - | 9 | = | 40 | 81 | 1600 | 1681 | 41 | |
| 49 | - | 21 | = | 28 | 441 | 784 | 1225 | 35 | |
| 289 | - | 85 | 204 | 7225 | 41616 | 48841 | 221 | ||
| 289 | - | 133 | 156 | 17689 | 24336 | 42025 | 205 | ||
| 441 | - | 81 | 360 | 6561 | 129600 | 136161 | 369 | ||
| 441 | - | 189 | 252 | 35721 | 63504 | 99225 | 315 | ||
| 529 | - | 184 | 345 | 33856 | 119025 | 152881 | 391 | ||
| 529 | - | 189 | 340 | 35721 | 115600 | 151321 | 389 | ||
| 961 | - | 217 | 744 | 47089 | 553536 | 600625 | 775 | ||
| 961 | - | 400 | 561 | 160000 | 314721 | 474721 | 689 | ||
| 1225 | - | 225 | 1000 | 50625 | 1000000 | 1050625 | 1025 | ||
| 1225 | - | 525 | 700 | 275625 | 490000 | 765625 | 875 | ||
| www.osfantasticosnumerosprimos.com.br | |||||||||
A tabela a seguir foi gerada a partir dos números ímpares de 1 a 1500:
a) elevou-se cada número ímpar ao quadrado (B);
b) gerou-se os 2 números triangulares consecutivos que somam os respectivos quadrados perfeitos (C e D);
c) elevou-se cada número triangular ao quadrado (E e F);
d) somou-se cada dupla de triangular ao quadrado, obtendo-se assim a soma de 2 quadrados de Triangulares Consecutivos (G);
e) extraiu-se a raiz quadrada de cada soma de 2 quadrados de triangulares consecutivos (H).
| Soma de 2 Quadrados | |||||||
| de Triangulares Consecutivos | |||||||
| A | B | C | D | E | F | G | H |
| ímpares | quadrado | triangulares | quadrado | quadrado | soma | raiz | |
| consecutivos | de 2 | quadrada | |||||
| quadrados | |||||||
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 7 | 49 | 21 | 28 | 441 | 784 | 1225 | 35 |
| 41 | 1681 | 820 | 861 | 672400 | 741321 | 1413721 | 1189 |
| 239 | 57121 | 28441 | 28680 | 808890481 | 822542400 | 1631432881 | 40391 |
| 1393 | 1940449 | 969528 | 970921 | 939984542784 | 942687588241 | 1882672131025 | 1372105 |
| www.osfantasticosnumerosprimos.com.br | |||||||
A Soma de 2 Quadrados de Triangulares Consecutivos apresentam as seguintes propriedades:
a) a coluna A são termos de ordem ímpares do Algoritmo Escada de Theon, isto é, termos b;
b) a coluna B, são os quadrados dos termos b do Algoritmo Escada de Theon;
c) a coluna G são números triangulares quadrados perfeitos do Algoritmo Escada de Theon;
d) coluna H são números que são produtos dos termos a por b do Algoritmo Escada de Theon.
A Soma de 2 Quadrados de Triangulares Consecutivos apresentam também propriedades matemáticas inéditas na qual determinada soma de 2 quadrados de triangulares consecutivos geram:
a) números triangulares quadrados perfeitos
e
b) ternos pitagóricos triangulares quase-perfeitos em que os temos a e b são números triangulares consecutivos (respectivamente os catetos de triângulo retângulo) e o termo c (hipotenusa) um termo do Algoritmo Escada de Theon, propriedades estas que podem ser constatadas na seguinte tabela:
| Ternos Pitagóricos | |||||
| Triangulares Quase Perfeitos | |||||
| triangulares | termos | quadrado | quadrado | soma de | |
| consecutivos | de | de | de | 2 | |
| Theon | quadra- | ||||
| a | b | c | a | b | dos |
| (triangular | |||||
| quadrado | |||||
| perfeito) | |||||
| 21 | 28 | 35 | 441 | 784 | 1225 |
| 820 | 861 | 1189 | 672400 | 741321 | 1413721 |
| 28441 | 28680 | 40391 | 808890481 | 822542400 | 1631432881 |
| 969528 | 970921 | 1372105 | 939984542784 | 942687588241 | 1882672131025 |
| www.osfantasticosnumerosprimos.com.br | |||||
Se a soma dos quadrados de 2 números triangulares consecutivos tiver como resultado um quadrado perfeito, então esse quadrado é um número triangular quadrado perfeito e a sua raiz quadrada é um termo do Algoritmo Escada de Theon.
28 - 21 = 7
7 é raiz quadrada da soma dos triangulares 21 e 28
21 + 28 = 49
7 é um termo do Algoritmo Escada de Theon
861 - 820 = 41
41 é raiz quadrada da soma dos triangulares 820 e 861
820 + 861 = 1189
41 é um termo do Algoritmo Escada de Theon
28680 - 28441 = 239
239 é raiz quadrada da soma dos triangulares 28441 e 28680
28441 + 28680 = 57121
239 é um termo do Algoritmo Escada de Theon
970921 - 969528 = 1393
1393 é raiz quadrada da soma dos triangulares 969528 e 970921
969528 + 970921 = 1940449
1393 é um termo do Algoritmo Escada de Theon
Autor: Ricardo Silva - setembro/2025
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato