


Número Par é um número que ao ser dividido por 2 deixa resto 0 (zero).
Número Quadrado Perfeito é um número que é produto de um número por ele mesmo e quando extraída a sua raiz quadrada o resultado é um número inteiro.
O presente estudo demonstram métodos de como se gerarem números quadrados perfeitos através da soma de grupos de números pares consecutivos.
A Tabela 1 apresenta os 31 primeiros números pares com suas respectivas ordens / posições.
As ordens / posições (destacadas em laranja) formam uma Progressão Aritmética - P.A. cujo primeiro termo é 3 e razão 4: 3, 7, 11, 15,...
Os números pares (destacados em laranja) formam uma Progressão Aritmética - P.A. cujo primeiro termo é 4 e razão 8: 4, 12, 20, 28,...
| Tabela 1 | |
| Ordens / Posições de Números Pares | |
| ordem / posições | números pares |
| 1 | 0 |
| 2 | 2 |
| 3 | 4 |
| 4 | 6 |
| 5 | 8 |
| 6 | 10 |
| 7 | 12 |
| 8 | 14 |
| 9 | 16 |
| 10 | 18 |
| 11 | 20 |
| 12 | 22 |
| 13 | 24 |
| 14 | 26 |
| 15 | 28 |
| 16 | 30 |
| 17 | 32 |
| 18 | 34 |
| 19 | 36 |
| 20 | 38 |
| 21 | 40 |
| 22 | 42 |
| 23 | 44 |
| 24 | 46 |
| 25 | 48 |
| 26 | 50 |
| 27 | 52 |
| 28 | 54 |
| 29 | 56 |
| 30 | 58 |
| 31 | 60 |
| www.osfantasticosnumerosprimos.com.br | |
Pode-se também obter a Progressão Aritmética: 4, 12, 20, 28,... por meio de multiplicações do número 4 com a sequência de números ímpares.
| Tabela 2 | ||||
| Progressão Aritmética 4, 12, 20, 28,... | ||||
| números ímpares | produto | |||
| 4 | x | 1 | = | 4 |
| 4 | x | 3 | = | 12 |
| 4 | x | 5 | = | 20 |
| 4 | x | 7 | = | 28 |
| 4 | x | 9 | = | 36 |
| 4 | x | 11 | = | 44 |
| 4 | x | 13 | = | 52 |
| 4 | x | 15 | = | 60 |
| 4 | x | 17 | = | 68 |
| 4 | x | 19 | = | 76 |
| 4 | x | 21 | = | 84 |
| 4 | x | 23 | = | 92 |
| 4 | x | 25 | = | 100 |
| 4 | x | 27 | = | 108 |
| 4 | x | 29 | = | 116 |
| 4 | x | 31 | = | 124 |
| 4 | x | 33 | = | 132 |
| 4 | x | 35 | = | 140 |
| 4 | x | 37 | = | 148 |
| 4 | x | 39 | = | 156 |
| 4 | x | 41 | = | 164 |
| 4 | x | 43 | = | 172 |
| 4 | x | 45 | = | 180 |
| 4 | x | 47 | = | 188 |
| 4 | x | 49 | = | 196 |
| 4 | x | 51 | = | 204 |
| 4 | x | 53 | = | 212 |
| 4 | x | 55 | = | 220 |
| 4 | x | 57 | = | 228 |
| 4 | x | 59 | = | 236 |
| 4 | x | 61 | = | 244 |
| www.osfantasticosnumerosprimos.com.br | ||||
Observação importante: por questões didáticas e de organização, o presente triângulo está sendo nomeado de: Triângulo Numérico 14.
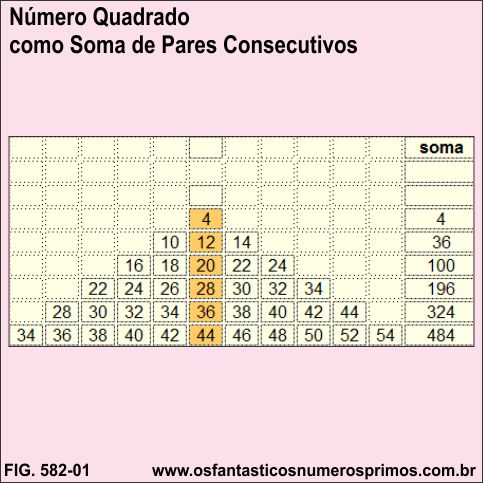
Construindo-se um triângulo numérico cuja altura é formada pela Progressão Aritmética: 4, 12, 20, 28, 36,... e suas linhas partindo-se do 4, com quantidades ímpares de termos, verifica-se que as somas de cada uma das linhas, têm como resultados números quadrados perfeitos pares cujas raízes quadradas são dobros de números ímpares..
| Triângulo Numérico 14 | ||||||||||||
| Progressão Aritmética Central | ||||||||||||
| 4, 12, 20, 28, 36, ... | ||||||||||||
| soma | raiz | |||||||||||
| quadrada | ||||||||||||
| 4 | 4 | 2 | ||||||||||
| 10 | 12 | 14 | 36 | 6 | ||||||||
| 16 | 18 | 20 | 22 | 24 | 100 | 10 | ||||||
| 22 | 24 | 26 | 28 | 30 | 32 | 34 | 196 | 14 | ||||
| 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 44 | 324 | 18 | ||
| 34 | 36 | 38 | 40 | 42 | 44 | 46 | 48 | 50 | 52 | 54 | 484 | 22 |
| www.osfantasticosnumerosprimos.com.br | ||||||||||||
Interessante observar que as somas de termos da altura do triângulo são números quadrados perfeitos da seguinte forma:
a) quando a quantidade de termos é potência de base 2, as somas são quadrados perfeitos de potências de base 2;
Exemplos:
4
4 + 12 = 16
4 + 12 + 20 + 28 = 64
b) quando a quantidade de termos não é potência de base 2, as somas são quadrados perfeitos, mas não de potências de base 2.
4 + 12 + 20 = 36
4 + 12 + 20 + 28 + 36 = 100
Um fato a ser destacado é que o Triângulo Numérico 14 é o primeiro triângulo numérico publicado aqui no WebSite Os Fantásticos Números Primos e nos livros digitais, aqui divulgados, cujo lado direito "diagonais direita", os números têm terminações com os mesmos algarismos, formando Progressões Aritméticas de razão 10.
c) cada termo da sequência: 4, 12, 20, 28, 36,... são partes de um quadrado perfeito;
Exemplos:
4 x 3 = 12
12 é 1/3 do quadrado 36
4 x 5 = 20
20 é 1/5 do quadrado 100
4 x 7 = 28
28 é 1/7 do quadrado 196
d) Os quadrados 4, 36, 100, 196, 324, 484, ... são somas de 4 quadrados ímpares;
Exemplos:
1 + 1 + 1 + 1 = 4
9 + 9 + 9 + 9 = 36
25 + 25 + 25 + 25 = 100
O Método abaixo, foi enviado pelo Professor de Química Fernando Manso, da Universidade Tecnológica Federal do Paraná - UTFPR-CM.
"Método para encontrar quadrados perfeitos como a soma de pares consecutivos:
1) número de pares consecutivos a serem somados: n=2j+1;
2) Termo central ak = 4(2j+1);
3) O quadrado obtido pela soma de n números pares consecutivos:
Q = (4j+2)^2. j é um número natural.
Escolha um valor qualquer para j e, a partir do termo central, construa a sequência de números pares consecutivos cuja soma será um quadrado perfeito.
Ex: j=3;
n=2j+1=2x3+1=7, teremos que somar 7 números pares consecutivos;
ak = 4(2j+1) = 4(2x3+1)=4x7=28.
Esse é o número par que ocupará a posição central na sequência de números pares.
O quadrado obtido pela soma será Q = (4j+2)^2 = (4x3+2)^2=14^2=196.
Então temos:
sequência: 22, 24, 26, 28, 30, 32, 34:
22 + 24 + 26 + 28 + 30 + 32 + 34 = 3 x 56 + 28 = 168 + 28 = 196."
Autor: Ricardo Silva - agosto/2025
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato