capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página Textos

Triângulo Pitagórico 3-4-5 inscrito numa semicircunferência - 018

Nesses dias de quarentena, isto é, confinamento em que como eu e outras milhares de pessoas estão em suas residências, para tentar se previnir da contaminação por Coronavírus, pus me a pensar, a questionar...

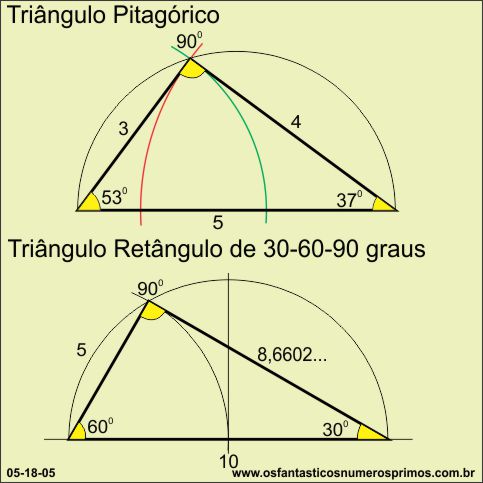
...será que é possível construir com régua não graduada e compasso um triângulo pitagórico 3-4-5 inscrito numa semicircunferência, semelhante a um triângulo equilátero inscrito numa circunferência ou um triângulo retângulo de 30, 60 e 90 graus inscrito numa semicircunferência?

Fazendo pesquisas na Word Wide Web com a palavra-chave "Triângulo Pitagórico inscrito numa semicircunferência". Encontrei sim, exemplos de triângulos pitagóricos 3-4-5 em que se deveriam descobrir medidas de lados ou relações métricas entre lados e projeções dos catetos sobre a hipotenusa.

No estudo:

005-texto-017-triangulo-pitagorico-inscrito-semicircunferencia

são apresentadas 3 novas relações métricas no triângulo retângulo escaleno que não são mencionadas, pelos menos, em duas coleções de livros didáticos de matemática dos anos de 2009 e 2010 que possuo.

Triângulo Pitagórico 3-4-5 e divisão do diâmentro em partes iguais

Aplicando a divisão de um segmento em partes iguais em um diâmetro arbitrário de uma semicircunferência, foi possível determinar conjuntamente os pontos que incidem também sobre a hipotenusa do triângulo retângulo 3-4-5 a ser inscrito.

A divisão de um segmento em partes iguais é uma aplicação do Teorema da Intersecção, conhecido também como Feixe de Retas Paralelas, teorema este creditado ao filósofo grego, Tales de Mileto.

Terminada a divisão geometricamente, o diâmetro ficou divido em 5 partes, isto é, com a medida de 5 unidades.

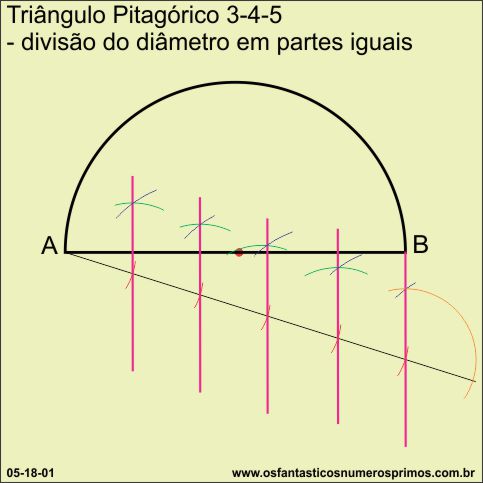
Triângulo Pitagórico 3-4-5 - divisão em partes iguais

Triângulo Pitagórico 3-4-5 e o cateto menor

Com a ponta seca no ponto A (extremidade esquerda do diâmetro) e abertura de 3 unidades, traça-se um arco de encontro com a semicircunferência e marca-se o ponto C.

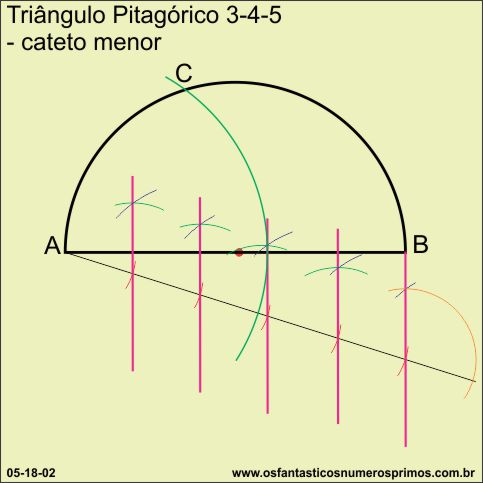
Triângulo Pitagórico 3-4-5 - cateto menor

Triângulo Pitagórico 3-4-5 e o cateto maior

Com a ponta seca no ponto B (extremidade direita do diâmetro) e abertura de 4 unidades, traça-se um arco de encontro com a semicircunferência no ponto C.

Triângulo Pitagórico 3-4-5

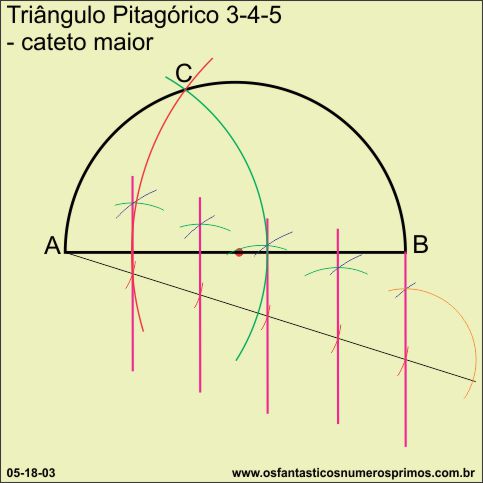
Unindo-se os pontos A, B e C, circunscreve-se então um triângulo pitagórico 3-4-5 em uma semicircunferência.

Triângulo Pitagórico e Triângulo Retângulo de 30-60-90 graus

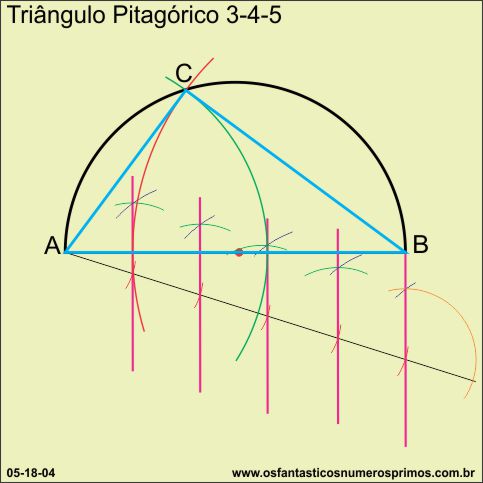
Comparando-se as propriedades intrínsicas entre triângulo pitagórico e triângulo retângulo de ângulos de 30, 60 e 90 graus podemos destacar que:

Triângulo pitagórico possui:

a) lados de números inteiros;

b) ângulos agudos com graus variáveis;

c) lados formados por terno pitagórico.

Triângulo retângulo de ângulos de 30, 60 e 90 graus possui:

a) cateto menor e hipotenusa com números inteiros;

b) cateto maior com número irracional;

c) ângulos agudos com graus fixos: 30 e 60 graus;

d) pontos notáveis quando inscritos numa semicircunferência;

e) ângulos submúltiplos de 360;

f) hipotenusa com o dobro do cateto menor;

g) cateto menor com a metade da hipotenusa.

Triângulo Pitagórico e Triângulo Retângulo de 30-60-90 graus

Desafio ao visitante

O Web-Site Os Fantásticos Números Primos lança um desafio a você estimado visitante: de construir um triângulo pitagórico inscrito numa circunferência somente com régua não graduada e compasso semelhante ao triângulo retângulo de 30, 60 e 90 graus para ser publicado na Seção Texto do WebSite.

Enviando o seu estudo e modelo matemático da sua solução, para o nosso e:mail:

contato@osfantasticosnumerosprimos.com.br,

você receberá como cortesia:

O livro digital OS FANTÁSTICOS NÚMEROS PRIMOS

Veja as matérias:

005-texto-017-triangulos-pitagoricos-inscrito-semicircunferencia

005-texto-018-triangulo-pitagorico3-4-5-inscrito-semicircunferencia

sobre construções de triângulos.

Autor: Ricardo Silva - abril/2020