


Teorema de Gou-gu é nome com o qual os antigos chineses denominavam o Teorema de Pitágoras, várias demonstrações com triângulos retângulos aparecem no livro Chou Pei Suan Ching, entre elas, um quadrado quadriculado de lado 7 por 7 no qual se encontra inscrito um quadrado de área 25 formado por 4 triângulos retângulos cujas hipotenusas são os lados do quadrado inscrito e cujo centro há um quadrado central de lado unitário.
O quadrado inscrito se assemelha há um catavento estelizado.

Fonte: https://pt.wikipedia.org
Cada triângulo retângulo possui a seguinte área:
3 x 4 = 12
12 / 2 = 6
Reparar que há um quadradinho no centro do quadrado inscrito.
Então, 4 triângulos x 6 (áreas) = 24
24 + 1 (quadradinho central) = 25 (área do quadrado inscrito)
O presente estudo demonstram que a partir do Teorema de Gou-gu são possíveis de se extrairem Números de Fermat da forma 4x + 1.
Pierre de Fermat, jurista e entusiasta matemático francês, (1601-1665), entre várias contribuições à Matemática, em carta a Marin Mersenne (1588-1648), datada de 25 de dezembro de 1640, afirma que números primos da forma 4x + 1 podem ser escritos como a soma de 2 quadrados enquanto números da forma 4x + 3 não podem ser escritos como a soma de 2 quadrados.
Números da forma 4x + 1 são divisíveis por 4.
Número primo da forma 4x + 1 pode ser escrito como soma de 2 quadrados.
Determinados números compostos da forma 4x + 1 podem ser escritos com mais de uma dupla de soma de 2 quadrados.
Exemplo:
1² + 8² = 1 + 64 = 65
4² + 7² = 16 + 49 = 65
Nem todo número composto da forma 4x + 1 pode ser escrito como soma de 2 quadrados.
Exemplos:
21, 33, 57, 69, 77, ... e outros.
No quadrado quadriculado de lado 3 e área 9, qual é a área e o lado do quadrado verde inscrito ?
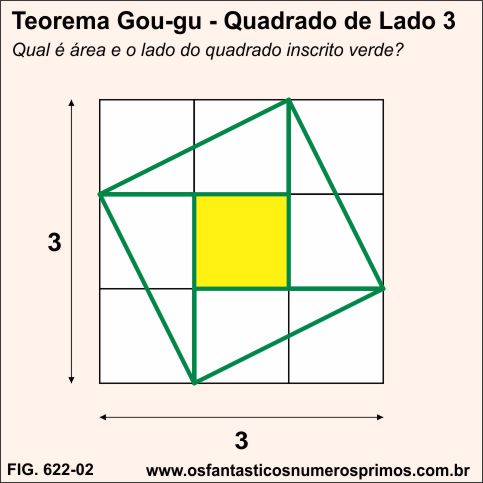
i) área de triângulo: (base x altura) / 2
( 2 x 1 ) / 2 = 1
ii) 4 (triângulos) x 1 = 4
iii) área do quadrado central = 1 x 1 = 1
iv) a área do quadrado verde é igual a 5cm² (4 + 1) e a medida do seu lado é √5 = 2,23...
A área 5 é um Número de Fermat da forma 4x + 1.
i) quadradinho central de área 1 subtraído do quadrado de área 9;
9 - 1 = 8
ii) a diferença 8 dividida por 2, tem como quociente um múltiplo de 4;
8 / 2 = 4
iii) o quociente 4 somado com o quadradinho de área 1 tem como resultado o quadrado inscrito de área 5;
4 + 1 = 5
A área 5 é um Número de Fermat da forma 4x + 1.
i) as medidas dos catetos elevados ao quadrado e somadas;
1² + 2² = 1 + 4 = 5
ii) 5 pode ser escrito como a soma de 2 quadrados, o 1 e o 4.
Observação importante: o número 3 pode ser obtido por meio das seguintes adições:
0 + 3 = 3
1 + 2 = 3
As parcelas 1 e 2 da segunda adição têm correspondências com as medidas dos catetos dos triângulos retângulos.
No quadrado quadriculado de lado 5 e área 25, qual é a área e o lado do quadrado azul inscrito ?
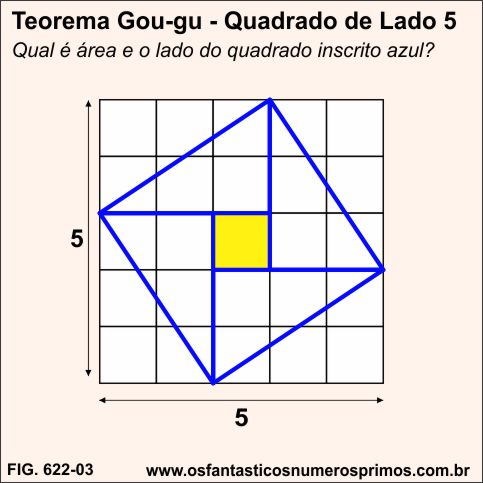
i) área de triângulo: (base x altura) / 2
( 2 x 3 ) / 2 = 3
ii) 4 (triângulos) x 3 = 12
iii) área do quadrado central = 1 x 1 = 1
iv) a área do quadrado azul é igual a 13cm² (12 + 1) e a medida do seu lado é √13 = 3,60...
A área 13 é um Número de Fermat da forma 4x + 1.
i) quadradinho central de área 1 subtraído do quadrado de área 25;
25 - 1 = 24
ii) diferença 24 dividida por 2, tem como quociente um múltiplo de 4;
24 / 2 = 12
iii) quociente 12 somado com o quadradinho de área 1 tem como resultado o quadrado inscrito de área 13;
12 + 1 = 13
A área 13 é um Número de Fermat da forma 4x + 1.
i) as medidas dos catetos elevados ao quadrado e somadas;
2² + 3² = 4 + 9 = 13
ii) 13 pode ser escrito como a soma de 2 quadrados, o 4 e o 9.
Observação importante: o número 5 pode ser obtido por meio das seguintes adições:
0 + 5 = 5
1 + 4 = 5
2 + 3 = 5
As parcelas 2 e 3 da terceira adição têm correspondências com as medidas dos catetos dos triângulos retângulos.
No quadrado quadriculado de lado 5 e área 25, qual é a área e o lado do quadrado vermelho inscrito ?
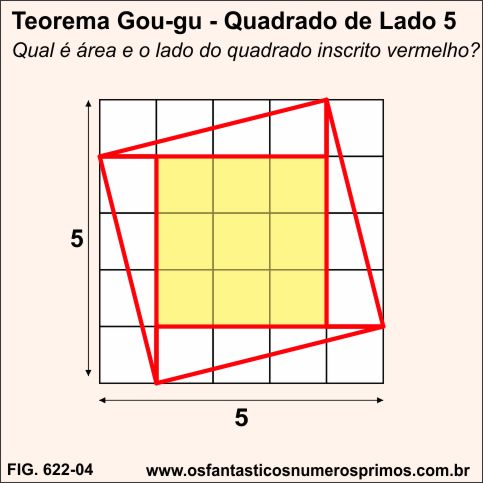
i) área de triângulo: (base x altura) / 2
( 1 x 4 ) / 2 = 2
ii) 4 (triângulos) x 2 = 8
iii) área do quadrado central = 3 x 3 = 9
iv) a área do quadrado vermelho é igual a 17cm² (8 + 9) e a medida do seu lado é √17 = 4,12...
A área 17 é um Número de Fermat da forma 4x + 1.
i) quadrado de área 9 subtraído do quadrado de área 25;
25 - 9 = 16
ii) diferença 16 dividida por 2, tem como quociente um múltiplo de 4;
16 / 2 = 8
iii) quociente 8 somado com o quadrado de área 9 tem como resultado o quadrado inscrito de área 17;
8 + 9 = 17
A área 17 é um Número de Fermat da forma 4x + 1.
i) as medidas dos catetos elevados ao quadrado e somados;
1² + 4² = 1 + 16 = 17
ii) 17 pode ser escrito como a soma de 2 quadrados, o 1 e o 4.
Observação importante: o número 5 pode ser obtido por meio dos seguintes adições:
0 + 5 = 5
1 + 4 = 5
2 + 3 = 5
As parcelas 1 e 4 da segunda adição têm correspondências com as medidas dos catetos dos triângulos retângulos.
Em quadrado quadriculado de lado 7 são possíveis de se inscreverem 3 quadrados (verde, azul e vermelho) e também 3 quadrados perfeitos centrais: 1, 9 e 16.
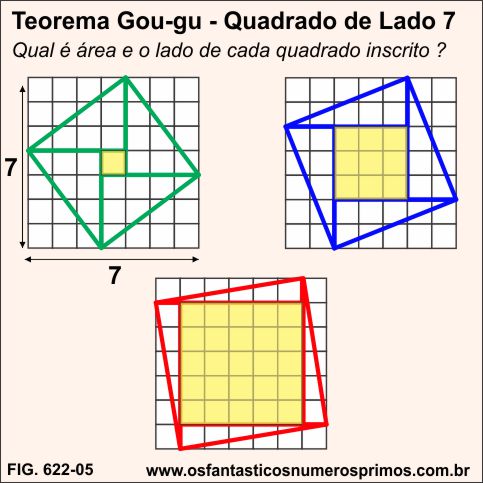
Observação importante: o número 7 pode ser obtido por meio das seguintes adições:
0 + 7 = 7
1 + 6 = 7
2 + 5 = 7
3 + 4 = 7
Os pares de parcelas a partir da segunda adição têm correspondências com as medidas dos catetos dos triângulos retângulos.
Os pares de parcelas elevadas ao quadrado e somadas tem como resultados números da forma 4x + 1.
0² + 7² = 0 + 49 = 49
1² + 6² = 1 + 36 = 37
2² + 5² = 4 + 25 = 29
3² + 4² = 9 + 16 = 25
Em quadrado quadriculado de lado 9 são possíveis de se inscreverem 4 quadrados (verde, azul, vervelho e laranja) e também 4 quadrados perfeitos centrais: 1, 9, 16 e 25.
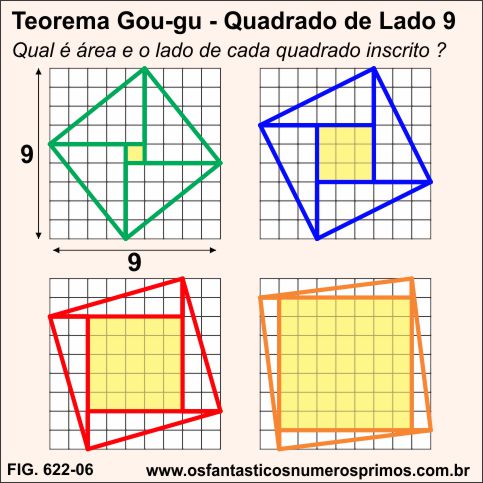
Observação importantíssima: o número 9 pode ser obtido por meio das seguintes adições:
0 + 9 = 9
1 + 8 = 9
2 + 7 = 9
3 + 6 = 9
4 + 5 = 9
Os pares de parcelas elevadas ao quadrado e somadas tem como resultados números da forma 4x + 1 e também são as medidas dos catetos dos triângulos retângulos, exceto o primeiro par 0 e 9.
0² + 9² = 0 + 81 = 81
1² + 8² = 1 + 64 = 65
2² + 7² = 4 + 49 = 53
3² + 6² = 9 + 36 = 45
4² + 5² = 16 + 25 = 41
Observação importante: o número 11 pode ser obtido por meio das seguintes adições:
0 + 11 = 11
1 + 10 = 11
2 + 9 = 11
3 + 8 = 11
4 + 7 = 11
5 + 6 = 11
Os pares de parcelas a partir da segunda adição têm correspondências com as medidas dos catetos dos triângulos retângulos.
Os pares de parcelas elevadas ao quadrado e somadas tem como resultados números da forma 4x + 1.
0² + 11² = 1 + 121 = 121
1² + 10² = 1 + 100 = 101
2² + 9² = 4 + 81 = 85
3² + 8² = 9 + 64 = 73
4² + 7² = 16 + 49 = 65
5² + 6² = 25 + 36 = 61
A tabela a seguir demonstram os 51 primeiros números ímpares e regularidades entre números da forma 4x + 1 que correspondem a lados de quadrados inscritos em quadrados com a utilização do Teorema de Gou-gu.
a) coluna A - ordem / posição de número ímpar;
b) coluna B - medida do lado do quadrado de Gou-gu;
c) coluna C - lado do quadrado inscrito no quadrado de Gou-gu;
a partir no número 5, há um número sim e outro não que subtraído 1 unidade é um número divisível por 4;
quadrado perfeito ímpar (laranja), a partir do quadrado 9, subtraído 1 é divisível por 4 e 8;
d) coluna D - quociente de número da coluna C menos 1 dividido por 4.
| Teorema de Gou-gu | ||||
| Quadrados Inscritos em Quadrados | ||||
| A | B | C | D | |
| ordem / | quadrado | lado | divisão | |
| posição | de lado | quadrado | por 4 | |
| inscrito | ||||
| 1 | 1 | 0 | ||
| 2 | 3 | |||
| 3 | 3 | gera | 5 | 1 |
| 4 | 7 | |||
| 5 | 9 | 2 | ||
| 6 | 11 | |||
| 7 | 5 | gera | 13 | 3 |
| 8 | 15 | |||
| 9 | 5 | gera | 17 | 4 |
| 10 | 19 | |||
| 11 | 21 | 5 | ||
| 12 | 23 | |||
| 13 | 7 | gera | 25 | 6 |
| 14 | 27 | |||
| 15 | 7 | gera | 29 | 7 |
| 16 | 31 | |||
| 17 | 33 | 8 | ||
| 18 | 35 | |||
| 19 | 7 | gera | 37 | 9 |
| 20 | 39 | |||
| 21 | 9 | gera | 41 | 10 |
| 22 | 43 | |||
| 23 | 9 | gera | 45 | 11 |
| 24 | 47 | |||
| 25 | 49 | 12 | ||
| 26 | 51 | |||
| 27 | 9 | gera | 53 | 13 |
| 28 | 55 | |||
| 29 | 57 | 14 | ||
| 30 | 59 | |||
| 31 | 11 | gera | 61 | 15 |
| 32 | 63 | |||
| 33 | 9, 11 | gera | 65 | 16 |
| 34 | 67 | |||
| 35 | 69 | 17 | ||
| 36 | 71 | |||
| 37 | 11 | gera | 73 | 18 |
| 38 | 75 | |||
| 39 | 77 | 19 | ||
| 40 | 79 | |||
| 41 | 81 | 20 | ||
| 42 | 83 | |||
| 43 | 11 | gera | 85 | 21 |
| 44 | 87 | |||
| 45 | 89 | 22 | ||
| 46 | 91 | |||
| 47 | 93 | 23 | ||
| 48 | 95 | |||
| 49 | 97 | 24 | ||
| 50 | 99 | |||
| 51 | 11 | gera | 101 | 25 |
| www.osfantasticosnumerosprimos.com.br | ||||
Pares de parcelas cujas adições têm como resultados números naturais ímpares quando elevados ao quadrado e somados têm como resultados Números de Fermat da Forma 4x + 1, esses pares de parcelas também são medidas de catetos de triângulos retângulos em construções de quadrados inscritos em quadrados com o Teorema de Gou-gu (excluindo pares em há o número 0 (zero) como primeira parcela).
Autor: Ricardo Silva - novembro/2025
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato