


Números da forma 4x + 1 são números múltiplos de 4 somado 1 unidade.
Entre os números da forma 4x + 1 há números primos e números compostos.
Pierre de Fermat, jurista e entusiasta matemático francês, (1601-1665), entre várias contribuições à Matemática, em carta a Marin Mersenne (1588-1648), datada de 25 de dezembro de 1640, afirma que números primos da forma 4x + 1 podem ser escritos como a soma de 2 quadrados enquanto números da forma 4x + 3 não podem ser escritos como a soma de 2 quadrados.[1]
Nos estudos publicados aqui no WebSite Os Fantásticos Números Primos:
011-estudos-590-algoritmo-da-soma-de-dois-numeros-quadrados-perfeitos
011-estudos-591-soma-de-dois-numeros-quadrados-perfeitos-e-algoritmo-s2q-2
são demonstrados respectivamente os Algoritmos S2Q1 e S2Q2 com os quais a partir de raízes e seus quadrados perfeitos ímpares são possíveis de se obterem Números de Fermat da forma 4x + 1, bem como, os 2 quadrados perfeitos que somados é esse número da forma 4x + 1
O presente estudo demonstram que a partir de números figurados quadrados perfeitos ímpares são possíveis de formarem números da forma 4x +1 em quadrados figurados ímpares maiores demarcando duplas de quadrados figurados menores, partindo-se da diagonal principal.
Números figurados, também denoninados de geométricos, são números que podem ser representados por meio de arranjos de pontos formando figuras geométricas e apresentam as seguintes classificações:
a) lineares - de uma só dimensão;
b) bidimensionais - de duas dimensões como: triângulos, quadrados, retângulos, etc...;
c) tridimensionais - de três dimensões como: pirâmides (números piramidais); poliedros (números poliédricos).
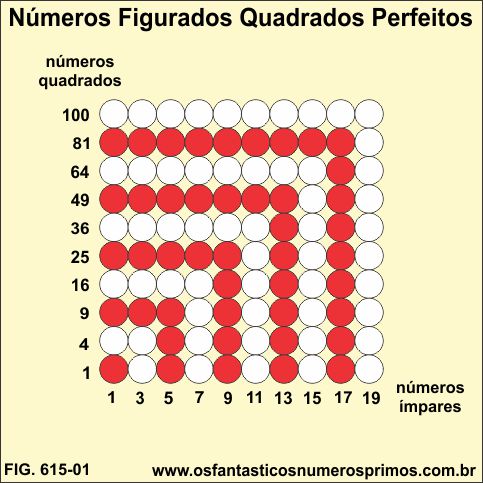
Partindo-se de 1 ponto e acrescentado sucessivamente quantidades ímpares de pontos, formam-se números figurados quadrados perfeitos sequencialmente.
No exemplos, os números figurados quadrados perfeitos de 1 a 100.
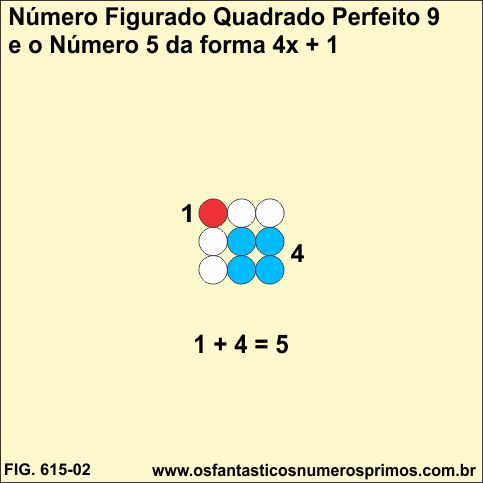
Partindo-se da diagonal principal e demarcando um ponto referente a um quadrado figurado 1 e 4 pontos referente a um quadrado figurado 4, forma-se o número 5 da forma 4x + 1 o qual pode ser escrito como soma de 2 quadrados.
1 + 4 = 5
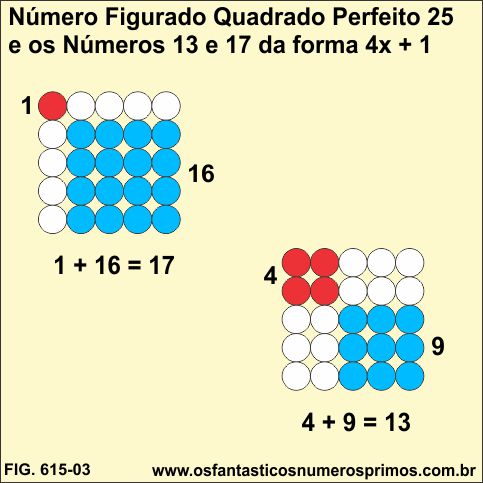
Com número figurado quadrado perfeito 25, obtêm-se os números 13 e 17 da forma 4x + 1 os quais podem ser escritos como soma de 2 quadrados.
1 + 16 = 17
4 + 9 = 13
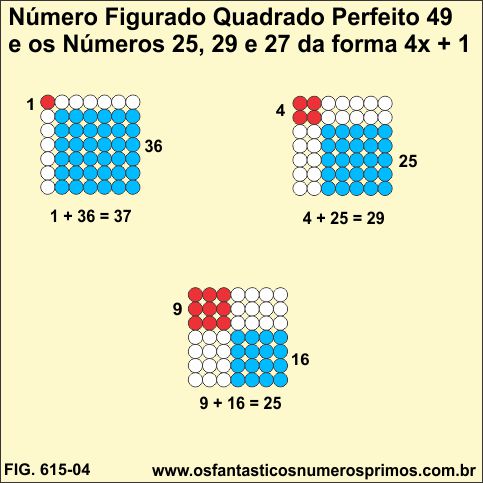
Com número figurado quadrado perfeito 49, obtêm-se os números 25, 29 e 37 da forma 4x + 1 os quais podem ser escritos como soma de 2 quadrados.
1 + 36 = 37
4 + 25 = 29
9 + 16 = 25
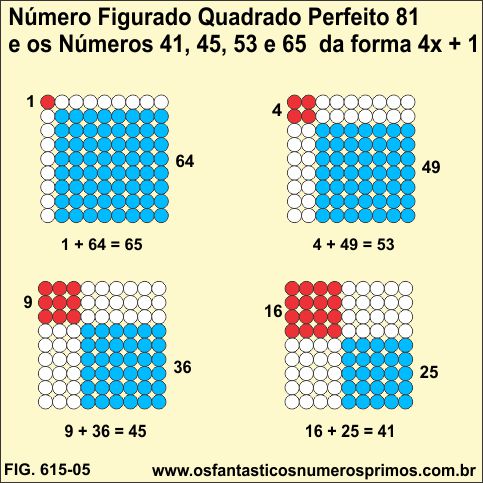
Com número figurado quadrado perfeito 81, obtêm-se os números 41, 45, 53 e 65 da forma 4x + 1 os quais podem ser escritos como soma de 2 quadrados.
1 + 64 = 65
4 + 49 = 53
9 + 36 = 45
16 + 25 = 41
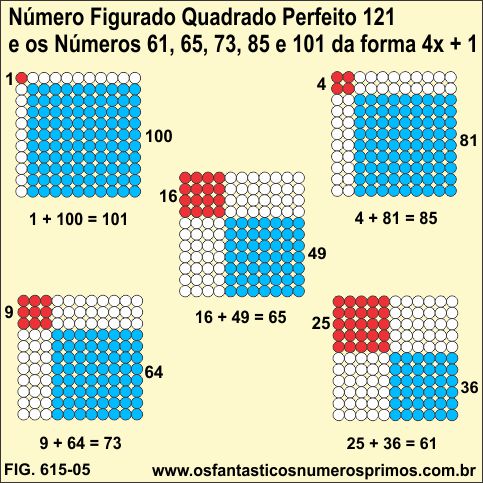
Com o número figurado quadrado perfeito 121, obtêm-se os números 61, 65, 73, 85 e 101 da forma 4x + 1 os quais podem ser escritos como soma de 2 quadrados.
1 + 100 = 101
4 + 81 = 85
9 + 64 = 73
25 + 36 = 61
Nos modelos matemáticos acima expostos, contata-se que a cada número figurado quadrado perfeito ímpar, as duplas de quadrados perfeitos figurados formam progressão aritmética de razão 1: 1, 2, 3, ...
A raíz quadrada de um quadrado perfeito ímpar subtraída 1 unidade têm como resultado a quantidade de quadrados perfeitos do quadrado 1 até esse quadrado ímpar cuja metade é a quantidade de duplas de quadrados.
As duplas de quadrados são formadas por quadrados equidistantes cujas soma são Números de Fermat da forma 4x + 1.
Interessante observar que:
a) as disposições dos quadrados formam triângulos isóceles (deitado);
b) as duplas são formadas por um quadrado constante e outro quadrado variável, isto é, as primeiras duplas tem como constante o quadrado 1, as segundas duplas, o quadrado 4 como constante e assim sucessivamente.
c) no quadrado figurado 25, a soma de cada dupla tem como resultado número primo, poderá haver somas cujos resultados são todos primos?
| Duplas de | ||||||||
| Números Quadrados Perfeitos | ||||||||
| Equidistantes | ||||||||
| 1a | 2a | 3a | 4a | 5a | 6a | 7a | ||
| dupla | dupla | dupla | dupla | dupla | dupla | dupla | ||
| quadrado | ||||||||
| figurado | 9 | |||||||
| 1 | 1 | |||||||
| 4 | 4 | |||||||
| 4x + 1 | soma | 5 | ||||||
| quadrado | 25 | |||||||
| figurado | ||||||||
| 1 | 1 | |||||||
| 4 | 4 | |||||||
| 9 | 9 | |||||||
| 16 | 16 | |||||||
| 4x + 1 | soma | 17 | 13 | |||||
| quadrado | 49 | |||||||
| figurado | ||||||||
| 1 | 1 | |||||||
| 4 | 4 | |||||||
| 9 | 9 | |||||||
| 16 | 16 | |||||||
| 25 | 25 | |||||||
| 36 | 36 | |||||||
| soma | 37 | 29 | 25 | |||||
| quadrado | 81 | |||||||
| figurado | ||||||||
| 1 | 1 | |||||||
| 4 | 4 | |||||||
| 9 | 9 | |||||||
| 16 | 16 | |||||||
| 25 | 25 | |||||||
| 36 | 36 | |||||||
| 49 | 49 | |||||||
| 64 | 64 | |||||||
| 4x + 1 | soma | 65 | 53 | 45 | 41 | |||
| quadrado | 121 | |||||||
| figurado | ||||||||
| 1 | 1 | |||||||
| 4 | 4 | |||||||
| 9 | 9 | |||||||
| 16 | 16 | |||||||
| 25 | 25 | |||||||
| 36 | 36 | |||||||
| 49 | 49 | |||||||
| 64 | 64 | |||||||
| 81 | 81 | |||||||
| 100 | 100 | |||||||
| 4x + 1 | soma | 101 | 85 | 73 | 65 | 61 | ||
| quadrado | 169 | |||||||
| figurado | ||||||||
| 1 | 1 | |||||||
| 4 | 4 | |||||||
| 9 | 9 | |||||||
| 16 | 16 | |||||||
| 25 | 25 | |||||||
| 36 | 36 | |||||||
| 49 | 49 | |||||||
| 64 | 64 | |||||||
| 81 | 81 | |||||||
| 100 | 100 | |||||||
| 121 | 121 | |||||||
| 144 | 144 | |||||||
| 4x + 1 | soma | 145 | 125 | 109 | 97 | 89 | 85 | |
| quadrado | 225 | |||||||
| figurado | ||||||||
| 1 | 1 | |||||||
| 4 | 4 | |||||||
| 9 | 9 | |||||||
| 16 | 16 | |||||||
| 25 | 25 | |||||||
| 36 | 36 | |||||||
| 49 | 49 | |||||||
| 64 | 64 | |||||||
| 81 | 81 | |||||||
| 100 | 100 | |||||||
| 121 | 121 | |||||||
| 144 | 144 | |||||||
| 169 | 169 | |||||||
| 196 | 196 | |||||||
| 4x + 1 | soma | 197 | 173 | 153 | 137 | 125 | 117 | 113 |
| www.osfantasticosnumerosprimos.com.br | ||||||||
A tabela a seguir apresenta as quantidades de duplas de números quadrados perfeitos geradas de cada número figurado quadrado perfeito ímpar, bem como, as quantidades de números primos das somas de 2 números quadrados perfeitos.
Em cada quantidade de duplas encontrou-se em média 3 números primos da forma 4x + 1.
| Soma de 2 Quadrados | |||
| e Números Primos | |||
| da forma 4x + 1 | |||
| raiz | quadrado | quantidade | quantidade |
| quadrada | perfeito | duplas | primos |
| 3 | 9 | 1 | 1 |
| 5 | 25 | 2 | 2 |
| 7 | 49 | 3 | 2 |
| 9 | 81 | 4 | 2 |
| 11 | 121 | 5 | 3 |
| 13 | 169 | 6 | 3 |
| 15 | 225 | 7 | 4 |
| 17 | 289 | 8 | 4 |
| 19 | 361 | 9 | 4 |
| 21 | 441 | 10 | 3 |
| 23 | 529 | 11 | 4 |
| 25 | 625 | 12 | 8 |
| 27 | 729 | 13 | 4 |
| 29 | 841 | 14 | 6 |
| 31 | 961 | 15 | 5 |
| 33 | 1089 | 16 | 4 |
| 35 | 1225 | 17 | 9 |
| 37 | 1369 | 18 | 6 |
| 39 | 1521 | 19 | 6 |
| 41 | 1681 | 20 | 9 |
| 43 | 1849 | 21 | 7 |
| 45 | 2025 | 22 | 7 |
| 47 | 2209 | 23 | 7 |
| 49 | 2401 | 24 | 5 |
| 51 | 2601 | 25 | 7 |
| 53 | 2809 | 26 | 9 |
| 55 | 3025 | 27 | 14 |
| 57 | 3249 | 28 | 8 |
| 59 | 3481 | 29 | 9 |
| 61 | 3721 | 30 | 11 |
| 63 | 3969 | 31 | 7 |
| 65 | 4225 | 32 | 17 |
| 67 | 4489 | 33 | 11 |
| 69 | 4761 | 34 | 10 |
| 71 | 5041 | 35 | 9 |
| 73 | 5329 | 36 | 13 |
| 75 | 5625 | 37 | 9 |
| 77 | 5929 | 38 | 7 |
| 79 | 6241 | 39 | 13 |
| 81 | 6561 | 40 | 9 |
| 83 | 6889 | 41 | 15 |
| 85 | 7225 | 42 | 20 |
| 87 | 7569 | 43 | 11 |
| 89 | 7921 | 44 | 14 |
| 91 | 8281 | 45 | 13 |
| 93 | 8649 | 46 | 8 |
| 95 | 9025 | 47 | 18 |
| 97 | 9409 | 48 | 14 |
| 99 | 9801 | 49 | 10 |
| 101 | 10201 | 50 | 18 |
| soma | 1275 | 419 | |
| www.osfantasticosnumerosprimos.com.br | |||
Autor: Ricardo Silva - novembro/2025
[1]NETO, Angelo Papa. Soma de 2 quadrados. IFCE
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato